Le 15 avril 2022 à 11:24:58 :
J'ai eu 9,5/10 khey merci

De rien, c’était quoi l’erreur ?

Le 15 avril 2022 à 14:55:22 :

Le 15 avril 2022 à 11:24:58 :
J'ai eu 9,5/10 khey merci

De rien, c’était quoi l’erreur ?

À la fin j'avais oublié de transformer Un+1 + U > 0 en Un+1 > U

tu peux faire mon dm de math stp mon reuf

et il y'a sa aussi c'est la partie 1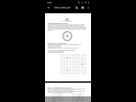

Merci au passage c'est pour lundi

1+1 ?

Alors stp fait le moi j'ai rien compris

Le 20 avril 2022 à 17:44:08 :
tu peux faire mon dm de math stp mon reuf

Le 20 avril 2022 à 17:44:43 :
et il y'a sa aussi c'est la partie 1

Partie 1

1.
Tu places ton rapporteur sur la ligne verticale passant par A, ensuite en te plaçant sur le point A, tu traces une droite dont l'angle entre le trait verticale et cette droite vaut 14°, cet angle est dirigé dans le sens horaire (à gauche par rapport au point A)
Tu fais la même chose avec le point B pour un angle de 72° et l'intersection des deux droites te donne un point C qui est la position du bateau.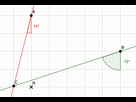

2.
Le point C se trouve à moins de deux carreaux de point R donc nous sommes en danger.

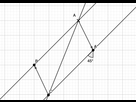
Partie 2.

Le vecteur correspond à une translation de 1 carreau vers la droite et 2 carreaux vers le bas.
On effectue cette translation sur le point A, ce qui nous donne le point A'.
Tu places ton rapporteur sur la ligne verticale passant par A', ensuite en te plaçant sur le point A, tu traces une droite dont l'angle entre le trait verticale et cette droite vaut 45°, cet angle est dirigé dans le sens horaire (à gauche par rapport au point A').
L'intersection entre cette droite que tu viens de tracer et la droite qui vise le point A à 22° te donnera le point C.
Pour obtenir le point B, tu effectues la translation inverse sur le point C, c'est à dire 2 carreaux vers le haut et un carreau vers la gauche à partir de point C, tu tomberas sur un point de la droite qui vise le point A à 45° et ce point c'est le point B

Merci mon frero

Le 22 avril 2022 à 05:37:04 :
Merci mon frero

Je t’en prie

Le 21 avril 2022 à 02:30:57 :
1+1 ?

Les axiomes de Peano :
1. L'élément appelé zéro et noté 0 est un entier naturel.
2. Tout entier naturel n a un unique successeur, noté s(n) ou Sn qui est un entier naturel.
3. Aucun entier naturel n'a 0 pour successeur.
4. Deux entiers naturels ayant le même successeur sont égaux.
5. Si un ensemble d'entiers naturels contient 0 et contient le successeur de chacun de ses éléments, alors cet ensemble est N.

On définit les entiers:
1 = S(0), 2 = S(1), 3 = S(2) etc...

On définit maintenant l'addition:
a + 0 = a
a + S(b) = S(a + b)

Alors:
1 + 1 = 1 + S(0) = S(1 + 0) = S(1) = 2

Up

Le 30 avril 2022 à 09:59:49 :
Up

je t'ai mp

Le 04 mai 2022 à 00:59:02 :
Voici l'op (Vecteurs):

Ce n'est pas précisé mais j'imagine que pour toutes les questions il faut calculer le produit scalaire vAB.vAC
(Quand je note vAB c'est pour désigner le vecteur AB et quand je note juste AB c'est pour désigner la longueur AB)

23.
Tu appliques la formule vAB.vAC = AB*AC*cos((vAB,vAC)) avec ta calculatrice réglée en mode degré
1.
vAB.vAC = 1*5*cos(40) ≃ 3,83
2.
vAB.vAC = 2,5*3*cos(70) ≃ 2,56
3.
vAB.vAC = 4*5/3*cos(-110) ≃ -2,28

24.
Même formule que pour 23., sauf que ici on est en radian, on peut donner une valeur exacte du cosinus de l'angle en regardant sur le cercle trigonométrique
1.
cos(pi/4) = racine(2)/2
vAB.vAC = 2*6*racine(2)/2 = 6*racine(2)
2.
cos(pi/6) = racine(3)/2
vAB.vAC = racine(3)*1*racine(3)/2 = 3/2
3.
cos(2*pi/3) = -1/2
vAB.vAC = 5*3/4*(-1/2) = -15/8

25.
Comme H est le projeté orthogonal de C sur (AB) alors :
- Si H appartient à [AB) alors l'angle BÂC est un angle aigu donc vAB.vAC = AB*AH
- Si H n'appartient pas à [AB) alors l'angle BÂC est un angle obtus donc vAB.vAC = -AB*AH
1.
H appartient à [AB)
vAB.vAC = AB*AH = 4*3 = 12
2.
H n'appartient pas à [AB)
vAB.vAC = -AB*AH = -1*5 = -5
3.
H n'appartient pas à [AB)
vAB.vAC = -AB*AH = -6*19/3 = -38

26.
Si on note vAB(x ; y) et vAC(x' ; y') les coordonnées des vecteurs vAB et vAC
Alors le produit scalaire est vAB.vAC = x*x' + y*y'
1.
vAB.vAC = 0*5 + (-2)*(-1) = 0 + 2 = 2
2.
vAB.vAC = 3*4 + 1*(-3) = 12 - 3 = 9
3.
vAB.vAC = 7*5 + (-4)*6 = 35 - 24 = 11

27.
Si ABC est un triangle quelconque on a alors
vAB.vAC = 1/2*(AB² + AC² - BC²)
1.
vAB.vAC = 1/2*(3² + 4² - 6²) = -11/2 = -5,5
2.
vAB.vAC = 1/2*(2² + (7/3)² - 1²) = 38/9 ≃ 4,22
3.
ABC est isocèle en A donc AC = AB = 5
vAB.vAC = 1/2*(5² + 5² - 2,5²) = 43,75/2 = 21,875

Up

t'es quelqu'un de bien je suis amoureuse

Salut comment je fais pour t'envoyer des images stp.

Ah c'est bon pourrais tu me faire ce dm merci urgent ?

Le 08 mai 2022 à 20:21:32 :

Ah c'est bon pourrais tu me faire ce dm merci urgent ?

Exercice 1

1)
a)
g’(x) = k.C.exp(k.x) = k.g(x)
g’ = k.g C’est donc bien une solution de l’équation y’ = k.y

1)
b)
g(0) = C = f(0)
g a les mêmes prorpiétés qie f

2)
a)
h’(x) = k’.C’.exp(k’.x) = k’.h(x)
Si on pose la condition k’ = k alors h’(x) = k.h(x) donc h est solution de y’ = k.y

2)
b)
h(0) = C’
Si on pose la condition C’ = C alors h(0) = C = f(0) donc h a les mêmes propriétés que f

2)
c)
h(x) = C.exp(k.x) = g(x)
Donc h = g

Exercice 2 1)

1)
a)
Delta = a^2 – 4.b > 0
Delta > 0 donc l’équation x^2 + a.x + b = 0 a deux solutions réelles qu’on note r1 et r2 et qui valent
r1 = (-a – racine(Delta))/2
r2 = (-a + racine(Delta))/2

1)
b)
r1 = r2 <=> racine(Delta) = 0 <=> Delta = 0
Or, Delta > 0 donc r1 =/= r2

1)
c) Pour cette partie de l’exercice je vais poser C = (r1.A – B)/(r1 – r2)
i) Il y a une faute dans l’énoncé, c’est « Montrer que g est solution de y’’ + a.y’ + b.y = 0 »
g(x) = (A – C).exp(r1.x) + C.exp(r2.x)
g’(x) = r1.(A – C).exp(r1.x) + r2.C.exp(r2.x)
g’’(x) = r1^2.(A – C).exp(r1.x) + r2^2.C.exp(r2.x)
g’’(x) + a.g’(x) + b.g(x) = (r1^2 + a.r1 + b).(A – C).exp(r1.x) + (r2^2 + a.r2 + b).C.exp(r2.x)
Comme r1 et r2 sont les solutions de x^2 + a.x + b = 0 alors (r1^2 + a.r1 + b) = 0 et (r2^2 + a.r2 + b) = 0 alors, g’’(x) + a.g’(x) + b.g(x) = 0
Donc g est solution de y’’ + a.y’ + b = 0

1)
c)
ii)
g(0) = A – C + C = A = f(0)
g’(0) = (r1^2.A – r1.r2.A)/(r1 – r2) - (r1^2.A - r1.B)/(r1 – r2) + (r1.r2.A – r2.B)/(r1 – r2) = (r1.B – r2.B)/(r1 – r2) = B = f’(0)
g a les mêmes propriétés que f

1)
d)
i)
h’(x) = alpha.C1.exp(alpha.x) + beta.C2.exp(beta.x)
h’’(x) = alpha^2.C1.exp(alpha.x) + beta^2.C2.exp(beta.x)
h’’(x) + a.h’(x) + b.h(x) = (alpha^2 + a.alpha + b). C1.exp(alpha.x) + (beta^2 + a.beta + b). C2.exp(beta.x)
En posant comme conditions alpha = r1 et beta = r2 on a alors (alpha^2 + a.alpha + b) = (r1^2 + a.r1 + b) = 0 et (beta^2 + a.beta + b) = (r2^2 + a.r2 + b) = 0 et donc h’’(x) + a.h’(x) + b.h(x) = 0
Aux conditions alpha = r1 et beta = r2, h est solution de y’’ + a.y’ + b.y = 0

1)
d)
ii)
On multiplie la première ligne par r1 et on la soustrait à la deuxième ligne :
r1.x + r2.y – r1.x – r1.y = A – r1.B <=> y.(r2 – r1) = A – r1.B <=> y = (A – r1.B)/(r2 – r1) <=> y = (r1.B – A)/(r1 – r2)
x + y = A <=> x = A – (r1.B – A)/(r1 – r2)

1)
d)
iii)
h(0) = C1 + C2
En posant les conditions C1 = x et C2 = y, h(0) = A = f(0)
Aux conditions alpha = r1 et beta = r2
h’(0) = r1.C1 + r2.C2
Aux conditions C1 = x et C2 = y, h’(0) = B = f(0)
Aux conditions C1 = x et C2 = y h a les mêmes propriétés que f

1)
d)
iv)
h(x) = (A – C).exp(r1.x) + C.exp(r2.x) = g(x)
Donc h = g

Exercice 2 2)
2)
a)
Delta = a^2 – 4.b = 0
Delta = 0 donc l’équation x^2 + a.x + b = 0 a une solution réelle qu’on note r0 et qui vaut
r0 = -a/2

2)
b) Pour cette partie de l’exercice je vais poser C = B – r0.A
i) Il y a une faute dans l’énoncé, c’est « Montrer que g est solution de y’’ + a.y’ + b.y = 0 »
g(x) = (C.x + A).exp(r0.x)
g’(x) = C.exp(r0.x) + r0.(C.x + A).exp(r0.x)
g’’(x) = 2.r0.C.exp(r0.x) + r0^2.(C.x + A).exp(r0.x)
g’’(x) + a.g’(x) + b.g(x) = (r0^2 + a.r0 + b).(C.x + A).exp(r0.x) + (a + 2.r0).C.exp(r0.x)
r0^2 + a.r0 + b = 0 car r0 est solution de x^2 + a.x + b = 0
a + 2.r0 = a + 2.(-a/2) = 0
Alors, g’’(x) + a.g’(x) + b.g(x) = 0
Donc g est solution de y’’ + a.y’ + b.y = 0

2)
b)
ii)
g(0) = A = f(0)
g’(0) = C + r0.A = B – r0.A + r0.A = B = f’(0)
g a les mêmes propriétés que f

2)
c)
i)
h’(x) = C1.exp(alpha.x) + alpha.(C1.x + C2).exp(alpha.x)
h’’(x) = 2.alpha.C1.exp(alpha.x) + alpha^2.(C1.x + C2).exp(alpha.x)
h’’(x) + a.h’(x) + b.h(x) = (alpha^2 + a.alpha + b).(C1.x + C2).exp(alpha.x) + (a + 2.alpha).C1.exp(alpha.x)
en posant la condition alpha = r0 on a
alpha^2 + a.alpha + b = r0^2 + a.r0 + b = 0
a + 2.alpha = a + 2.r0 = 0
Alors, h’’(x) + a.h’(x) + b.h(x) = 0
Sous la condition alpha = r0, h est solution de y’’ + a.y’ + b.y = 0

2)
c)
ii)
On multiplie la première ligne par r0 et on la soustrait à la deuxième ligne :
x + r0.y – r0.y = B – r0.A <=> x = B – r0.A

2)
c)
iii)
h(0) = C2
Si on pose la condition C2 = A alors h(0) = A = f(0)
h’(0) = C1 + alpha.C2
Sous les conditions alpha = r0 et C1 = A, si on pose la condition C2 = B alors
h’(0) = A + r0.B = B = f’(0)
Sous ces conditions, h a les mêmes propriétés que f

2)
c)
iv)
h(x) = ((B – r0.A).x + A).exp(r0.x) = g(x)
Donc h = g

:y