Le 30 avril 2024 à 17:46:23 :

1.a.
u(tau) = u(RC) = E*(1 - exp(-RC/RC)) = (1 - exp(-1))*E

1.b.
1 - exp(-1) = 0,63 à 10^-2 près
Donc u(tau) = 0,63*E
À l’instant tau, la tension du générateur est à 63% de ses capacités

2.
u(5tau) = u(5RC) = E*(1 - exp(-5RC/RC)) = (1 - exp(-5))*E
1 - exp(-5) = 0 ,99 à 10^-2 près
Donc u(5tau) = 0,99*E
Au bout de 5 tau, la tension du générateur est à 99% de ses capacités
Donc l’affirmation est vraie.

Le 01 mai 2024 à 19:26:26 :

1.
On pose u(x) = x^3 + 2
u’(x) = 3x^2
Alors, f(x) = u’(x)*u^4(x) = (1/5)*5*u’(x)*u^4(x)
Une primitive de f est donc F(x) = (1/5)*u^5(x)
F(x) = (1/5)*(x^3 + 2)^5

2.
On pose u(x) = 1 - 5x
u’(x) = -5
Alors, f(x) = u’(x)/u^2(x)
Une primitive de f est donc F(x) = -1/u(x)
F(x) = -1/(1 - 5x)

3.
On pose u(x) = x^2 + 2x + 2
u’(x) = 2x + 2
Alors, f(x) = u(x)/racine(u(x)) = 2*u(x)/(2*racine(u(x))
Une primitive de f est donc F(x) = 2*racine(u(u(x))
F(x) = 2*racine(x^2 + 2x + 2)

4.
On pose u(x) = 1/x
u’(x) = -1/x^2
Alors, f(x) = u’(x)*exp(u(x))
Une primitive de f est donc F(x) = exp(u(x))
F(x) = exp(1/x)

5.
On pose u(x) = -x^2
u’(x) = -2x
Alors, f(x) = -(3/2)*u’(x)*exp(u(x))
Une primitive de f est donc F(x) = -(3/2)*exp(u(x))
F(x) = -(3/2)*exp(-x^2)

Salut, tu pourrai me faire le 2 et le 3 de l'exercice 2 (le reste c'est déjà fait) et aussi l'exercice 3 stp ? J'en demande peut-être trop mais tu pourrai me le renvoyer avant 22h stp ? Merci d'avance car c'est un dm qui sauverai ma moyenne de maths et me permettrai d'aller en spé maths

Le 15 mai 2024 à 18:49:10 :

Exercice 2

1. On développe FC
f(x) = 2(x + 1)² - 1/2
= 2(x² + 2x + 1) - 1/2
= 2x² + 4x + 2 - 1/2
= 2x + 4x + 3/2

2. On développe FF
(2x + 3)(x + 1/2)
= 2x² + 3x + x + 3/2
= 2x² + 4x + 3/2
= f(x)

3.a) Pour f(0) on utilise FD et pour f(-3/2) on utilise FF
f(0)
= 2*0² + 4*0 + 3/2
= 0 + 0 + 3/2 = 3/2

f(-3/2)
= (2*(-3/2) + 3)*(-3/2 + 1/2)
= (-3 + 3)*(-3/2 + 1/2)
= 0*(-3/2 + 1/2)
= 0

3.b) On utilise FC
f(racine(3) - 1) = 2(racine(3) - 1 + 1)² - 1/2 = 2(racine(3))² - 1/2 = 2*3 - 1/2 = 6 - 1/2 = 11/2

3.c) On utilise FC
f(racine(3) + 1)
= 2(racine(3) + 1 + 1)² - 1/2
= 2(racine(3) + 2)² - 1/2
= 2(3 + 4racine(3) + 4) - 1/2
= 2(7 + 4racine(3)) - 1/2
= 14 + 8racine(3) - 1/2
= 27/2 + 8racine(3)

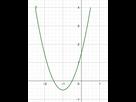
4.

6.

Exercice 3.

1)a)
g(-2)
= 1/2*(-2 + 3)² - 2
= 1/2*(1)² - 2
= 1/2 - 2
= -3/2

1)b)
g(racine(3))
= 1/2*(racine(3) + 3)² - 2
= 1/2*(3 + 6racine(3) + 9) - 2
= 1/2*(12 + 6racine(3)) - 2
= 6 + 3racine(3) - 2
= 4 + 3racine(3)

2)a)
g(x) = 0
<=> 1/2*(x + 3)² - 2 = 0
<=> 2*(1/2*(x + 3)² - 2) = 2*0
<=> (x + 3)² - 4 = 0

2)b) (erreur dans l’énoncé, c’est x = -5 et x = -1)
g(x) = 0
<=> (x + 3)² - 4 = 0
<=> (x + 3)² - 2² = 0
<=> (x + 3 - 2)(x + 3 + 2) = 0
<=> (x + 1)(x + 5) = 0
<=> x + 1 = 0 ou x + 5 = 0
<=> x = -1 ou x = -5
Les solutions de l’équation g(x) = 0 sont x = -5 et x = -1

Exercice 4

1)
3x² - 10x + 4 = 4
<=> 3x² - 10x + 4 - 4 = 0
<=> 3x² - 10x = 0
<=> x(3x - 10) = 0
<=> x = 0 ou 3x - 10 = 0
<=> x = 0 ou 3x = 10
<=> x = 0 ou x = 3/10
Les solutions sont x = 0 et x = 3/10

2)
(4x - 5)² - (4x - 5)(2x - 1) = 0
<=> (4x - 5)(4x - 5 - (2x - 1)) = 0
<=> (4x - 5)(4x - 5 - 2x + 1) = 0
<=> (4x - 5)(2x - 4) = 0
<=> 4x - 5 = 0 ou 2x - 4 = 0
<=> 4x = 5 ou 2x = 4
<=> x = 5/4 ou x = 2
Les solutions sont x = 5/4 et x =2

3)
(2x + 5)² = 81
<=> (2x + 5)² - 81 = 0
<=> (2x + 5)² - 9² = 0
<=> (2x + 5 - 9)(2x + 5 + 9) = 0
<=> (2x - 4)(2x + 14) = 0
<=> 2x - 4 = 0 ou 2x + 14 = 0
<=> 2x = 4 ou 2x = -14
<=> x = 2 ou x = -7
Les solutions sont x = -7 et x = 2

4)
(7x - 1)² - (3x + 1)² = 0
<=> (7x - 1 - (3x + 1))(7x - 1 + 3x + 1) = 0
<=> (7x - 1 - 3x - 1)(7x - 1 + 3x + 1) = 0
<=> (4x - 2)10x = 0
<=> 4x - 2 = 0 ou 10x = 0
<=> 4x = 2 ou x = 0
<=> x = 1/2 ou x = 0
Les solutions sont x = 0 et x = 1/2

Exercice 5

I)a)
14 mexicains sur 24 élèves
14/24 = 0,583 = 58,3% au dixième près
Environ 58,3% des élèves sont mexicains

I)b)
14 mexicains sur 24 élèves
75% des mexicains sont des filles
(14/24)*0,75 = 0,4375 = 43,75%
43,75% des élèves sont des filles mexicaines

II)1.
De 2021 à 2022 => 1 + 0,15 = 1,15 = 115% du prix de l’article
De 2022 à 2023 => 1 - 0,07 = 0,93 = 93% du prix de l’article
De 2021 à 2023 => 1,15*0,93 = 1,0695 = 106,95% du prix de l’article
Donc, de 2021 à 2023, le prix de l’article a augmenté de 6,95%

II)2.
En 2023, l’article est à 106,95% du prix de 2021.
En 2024, l’article doit diminuer de t pour retrouver le prix de 2021
De 2023 à 2024 => 1,0695(1 - t) = 1 = 100% du prix de l’article
1,0695(1 - t) = 1
<=> 1 - t = 1/1,0965
<=> -t = 1/1,0965 - 1
<=> t = 1 - 1/1,0965
t = 0,088 = 8,8% au dixième près.
De 2023 à 2024 le prix de l’article doit diminuer d’environ 8,8%

III)1.
La bague est constituée de 60% de cuivre
120*0,6 = 72g de cuivre
100g de cuivre coûte 2€
72g de cuivre coûte 2*72/100 = 1,44€

La bague étant uniquement constituée de cuivre et d’argent, on en déduit la masse d’argent utilisée qui est
120 - 72 = 48g d’argent
100g d’argent coûte 25€
48g d’agent coûte 25*48/100 = 12€

Le coût de fabrication de la bague est donc de 1,44 + 12 = 13,44€

III)2.
Augmentation de 15% sur le coût de fabrication de la bague
13,44*(1 + 0,15) = 13,44*1,15 = 15,46€ au centième près.
Le prix de vente de cette bague doit être de 15,46€

Salut mec ,
Voici l'exo et merci d'avance

Le 30 mai 2024 à 10:42:17 :
Salut mec ,
Voici l'exo et merci d'avance

Notations :

-A = A barre (l’événement contraire de A)
AnB = A et B (ou A inter B)
PB(A) = Probabilité que l’événement A se réalise sachant que B est réalisé

T : « La personne achète une télévision »
M : « La personne achète un magnétoscope »

P(T) = 0,6
P(-T) = 1 - 0,6 = 0,4
PT(M) = 0,4
PT(-M) = 1 - 0,4 = 0,6
P-T(M) = 0,2
P-T(-M) = 1 - 0,2 = 0,8

1.

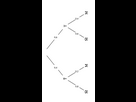
2.
D’après la formule des probabilités totales :
P(M) = P(TnM) + P(-TnM)
= P(T)*PT(M) + P(-T)*P-T(M)
= 0,6*0,4 + 0,4*0,2
= 0,24 + 0,08
= 0,32

3.
Je pense qu’il y a une erreur dans l’énoncé et qu’on veut plutôt savoir si on peut lire PM(T) sur l’arbre et non pas PT(M) (sinon la question n’a pas de sens pour moi)
La réponse est non, on ne peut pas lire PM(T) sur l’arbre.

4.
Je pense qu’il y a également une erreur ici et qu’on veut savoir si on peut calculer la probabilité PM(T) et non pas PT(M)
La réponse est oui,
PM(T) = P(MnT)/P(M)
= (P(T)*PT(M))/P(M)
= (0,6*0,4)/0,32
= 0,24/0,32
= 0,75

Topic toujours d'actualité

Salut khey
Tu pourrais simplifier ces deux expressions stp

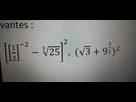
Le 19 septembre 2024 à 14:05:29 :
Salut khey
Tu pourrais simplifier ces deux expressions stp

Merci encore, tu nous sauve !

Le 23 septembre 2024 à 20:24:05 :

Merci encore, tu nous sauve !

J’écris z_ pour z barre (ou conjugué de z)

1)
On vérifie que le dénominateur ne s’annule pas

Soit z un complexe, c’est à dire qu’il existe des réels a et b tel que z = a + ib

zz_ + 1 = (a + ib)(a - ib) + 1 = a² - (ib)² + 1 = a² + b² + 1
zz_ + 1 est un réel > 0

z’ est bien défini quel que soit le complexe z

2)
Soit z un complexe, c’est à dire qu’il existe des réels a et b tel que z = a + ib

(z - z_)(z + z_) = z² - z_²

z² = (a + ib)² = a² + i2ab + (ib)² = a² + i2ab - b²
z_² = a² - i2ab + (ib)² = a² - i2ab - b²

z² - z_² = a² + i2ab - b² - (a² - i2ab - b²) = a² + i2ab - b² - a² + i2ab + b² = i4ab

Donc (z - z_)(z + z_) = i4ab

Dans la question 1), on a vu que zz_ + 1 est un réel.
Alors, z’ est un réel si et seulement si z² - 2i est un réel c’est à dire que sa partie imaginaire est nulle.

z² - 2i = a² + i2ab - b² - 2i = a² - b² + i2(ab - 1)

Supposons que z’ est un réel
<=> z² - 2i est un réel
<=> ab - 1 = 0
<=> ab = 1
<=> i4ab = 4i
<=> (z - z_)(z + z_) = 4i

3)
Soit z un complexe, c’est à dire qu’il existe des réels a et b tel que z = a + ib

Supposons que z’ est réel donc d’après la question 2)
<=> ab = 1
<=> a =/= 0 et b = 1/a

S = {z = a + i(1/a) , où a est un réel non nul}

Merci, j'ai eu 17 grâce à toi.
Cependant j'ai énormément de mal à comprendre la correction, possible de me l'expliquer ? Au moins pour l'exo 2 ?

Le 29 septembre 2024 à 21:35:14 :
Merci, j'ai eu 17 grâce à toi.
Cependant j'ai énormément de mal à comprendre la correction, possible de me l'expliquer ? Au moins pour l'exo 2 ?

Pour la question 2), on utilise le fait qu'un nombre complexe est un réel si et seulement si il est égal à son conjugué.

On exprime donc le conjugué de z' (c'est à dire z' barre) en fonction de z
Puis on remarque que z' = z'_ si leur numérateur sont égaux (car ils ont le même dénominateur).
On part donc de l'égalité entre les numérateurs et en manipulant un peu on fini par aboutir au résultat voulu.

Le 29 septembre 2024 à 23:32:52 :

Le 29 septembre 2024 à 21:35:14 :
Merci, j'ai eu 17 grâce à toi.
Cependant j'ai énormément de mal à comprendre la correction, possible de me l'expliquer ? Au moins pour l'exo 2 ?

Pour la question 2), on utilise le fait qu'un nombre complexe est un réel si et seulement si il est égal à son conjugué.

On exprime donc le conjugué de z' (c'est à dire z' barre) en fonction de z
Puis on remarque que z' = z'_ si leur numérateur sont égaux (car ils ont le même dénominateur).
On part donc de l'égalité entre les numérateurs et en manipulant un peu on fini par aboutir au résultat voulu.

D'accord, merci, je comprends mieux.

Le 30 septembre 2024 à 20:19:39 :

1.
Z = z² - 2iz + 2
= (x + iy)² - 2i(x + iy) + 2
= x² + 2ixy + (iy)² - 2ix - 2i²y + 2
= x² + 2ixy - y² - 2ix + 2y + 2 =
= x² - y² + 2y + 2 + i(2x(y - 1))

2.
Si z est imaginaire pur, alors z = iy (c'est à dire x = 0)
On reprend la forme algébrique de la question 1. on a :
Z = 0² - y² + 2y + 2 + i(2*0*(y - 1))
= -y² + 2y + 2 + i*0
= -y² + 2y + 2
Donc Z est un réel.

3.
On pose z = 1 + i (c’est à dire x = 1 et y = 1) qui n’est pas un imaginaire pur.
On reprend la forme algébrique de la question 1. on a :
Z = 1² - 1² + 2*1 + 2 + i(2*1(1 - 1))
= 1 - 1 + 2 + 2 + i*0
= 4
Z est un réel
Donc la réciproque n’est pas vraie.

4.
Z est un réel si et seulement si sa partie imaginaire est nulle
On reprend la forme algébrique de la question 1. Z est un réel si et seulement si
2x(y - 1) = 0
<=> 2x = 0 ou y - 1 = 0
<=> x = 0 ou y = 1
L’ensemble des nombres complexes z tel que Z soit réel est
E = {z = iy avec y un réel ou z = x + i avec x un réel}