Le 05 décembre 2023 à 18:39:26 :
bonsoir c'est ce dm merci d'avance

Déterminer le taux de variation

1.a.
Pour 0 pièce
C(0) = 100*racine(0) + 500 = 100*0 + 500 = 0 + 500 = 500 €
Pour 400 pièces
C(400) = 100*racine(400) + 500 = 100*20 + 500 = 200 + 500 = 700 €

1.b.
(C(400) - C(0))/(400 - 0) = (700 - 500)/(400 - 0) = 200/400 = 1/2

1.c.
coût de fabrication de 900 pièces
C(900) = 100*racine(900) + 500 = 100*30 + 500 = 300 + 500 = 800€

taux de variation du coût de fabrication entre 400 et 900 pièces
(C(900) - C(400))/(900 - 400) = (800 - 100)/(900 - 400) = 100/500 = 1/5

1/2 > 1/5, le coût de fabrication entre 0 et 400 pièces croît plus rapidement qu’entre 400 et 900 pièces.

2.a.
Cm(200) = C(200 + 1) - C(200) = C(201) - C(200) = 100*racine(201) + 500 - (100*racine(200) + 500) = 100*racine(201) + 500 - 100*racine(200) - 500 = 100*(racine(201) - racine(200)) = 3,53€ au centime près.

2.b.
Cm(800) = C(800 + 1) - C(800) = 100*(racine(801) - racine(800)) = 1,77 € au centime près.

2.c.
Cm(200) > Cm(800)

Taux de variation

1.1.a.
Entre -4 et -3 la courbe décroît donc le signe du taux de variation de f est négatif

1.1.b.
Entre 0 et 1 la courbe croît donc le signe du taux de variation de f est positif

1.1.c.
Entre 2 et 3 la courbe décroît donc le signe du taux de variation de f est négatif

1.1.d.
Entre 0 et 1 la courbe croît donc le signe du taux de variation de f est positif
Entre 1 et 3 la courbe décroît donc le signe du taux de variation de f est négatif

1.2.
Entre -4 e -3 et entre -2 et -1 f décroît donc le taux de variation de f est négatif dans les deux cas.

La courbe décroît plus vite entre -2 et -1 qu’entre -4 et -3 donc le taux de variation de f entre -4 et -3 est plus grand qu’entre -2 et -1.

2.1.
La fonction cube est la fonction f(x) = x^3

f(0) = 0^3 = 0
f(1) = 1^3 = 1
f(3) = 3^3 = 9

Taux de variation de la fonction cube entre 0 et 1
(f(1) - f(0))/(0 - 1) = (1 - 0)/(1 - 0) = 1/1 = 1

Taux de variation de la fonction cube entre 1 et 3
(f(3) - f(1))/(3 - 1) = (9 - 1)/(3 - 1) = 8/2 = 4

2.2.
La fonction inverse est la fonction g(x) = 1/x

g(0,1) = 1/0,1 = 10
g(1) = 1/1 = 1
g(10) = 1/10 = 0,1

Taux de variation de la fonction inverse entre 0,1 et 1
(g(1) - g(0,1))/(1 - 0,1) = (1 - 10)/(1 - 0,1) = -9/0,9 = -10

Taux de variation de la fonction inverse entre 1 et 10
(g(10) - g(1))/(10 - 1) = (0,1 - 1)/(10 - 1) = -0,9/9 = -0,1

Population de Floirac

1.
La courbe croît le plus rapidement entre 1968 et 1975, donc c’est la période pendant laquelle l’évolution de la population est la plus rapide

2.
On modélise la population de Floirac par une fonction P telle que P(x) représente le nombre d’habitants pour l’année x.

P(1968) = 8241
P(1990) = 16384
P(2007) = 15794

Le taux de variation de la population de Floirac entre 1968 et 1990 est
(P(1990) - P(1968))/(1990 - 1968) = (16384 - 8241)/(1990 - 1968) = 8143/22 = 370 (à l’unité près)

Le taux de variation de la population de Floirac entre 1990 et 2007 est
(P(2007) - P(1990))/(2007 - 1990) = (15794 - 16384)/(2007 - 1990) = -590/17 = -35 (à l’unité près)

Conclusion
Le taux de variation entre 1968 et 1990 étant positif, la population de Floirac croît lors de cette période.
Le taux de variation entre 1990 et 2007 étant négatif, la population de Floirac décroît lors de cette période.

Ce khey vertueux , ça m'émeus !

Le 06 décembre 2023 à 14:10:25 :

Le 05 décembre 2023 à 18:39:26 :
bonsoir c'est ce dm merci d'avance

Déterminer le taux de variation

1.a.
Pour 0 pièce
C(0) = 100*racine(0) + 500 = 100*0 + 500 = 0 + 500 = 500 €
Pour 400 pièces
C(400) = 100*racine(400) + 500 = 100*20 + 500 = 200 + 500 = 700 €

1.b.
(C(400) - C(0))/(400 - 0) = (700 - 500)/(400 - 0) = 200/400 = 1/2

1.c.
coût de fabrication de 900 pièces
C(900) = 100*racine(900) + 500 = 100*30 + 500 = 300 + 500 = 800€

taux de variation du coût de fabrication entre 400 et 900 pièces
(C(900) - C(400))/(900 - 400) = (800 - 100)/(900 - 400) = 100/500 = 1/5

1/2 > 1/5, le coût de fabrication entre 0 et 400 pièces croît plus rapidement qu’entre 400 et 900 pièces.

2.a.
Cm(200) = C(200 + 1) - C(200) = C(201) - C(200) = 100*racine(201) + 500 - (100*racine(200) + 500) = 100*racine(201) + 500 - 100*racine(200) - 500 = 100*(racine(201) - racine(200)) = 3,53€ au centime près.

2.b.
Cm(800) = C(800 + 1) - C(800) = 100*(racine(801) - racine(800)) = 1,77 € au centime près.

2.c.
Cm(200) > Cm(800)

Taux de variation

1.1.a.
Entre -4 et -3 la courbe décroît donc le signe du taux de variation de f est négatif

1.1.b.
Entre 0 et 1 la courbe croît donc le signe du taux de variation de f est positif

1.1.c.
Entre 2 et 3 la courbe décroît donc le signe du taux de variation de f est négatif

1.1.d.
Entre 0 et 1 la courbe croît donc le signe du taux de variation de f est positif
Entre 1 et 3 la courbe décroît donc le signe du taux de variation de f est négatif

1.2.
Entre -4 e -3 et entre -2 et -1 f décroît donc le taux de variation de f est négatif dans les deux cas.

La courbe décroît plus vite entre -2 et -1 qu’entre -4 et -3 donc le taux de variation de f entre -4 et -3 est plus grand qu’entre -2 et -1.

2.1.
La fonction cube est la fonction f(x) = x^3

f(0) = 0^3 = 0
f(1) = 1^3 = 1
f(3) = 3^3 = 9

Taux de variation de la fonction cube entre 0 et 1
(f(1) - f(0))/(0 - 1) = (1 - 0)/(1 - 0) = 1/1 = 1

Taux de variation de la fonction cube entre 1 et 3
(f(3) - f(1))/(3 - 1) = (9 - 1)/(3 - 1) = 8/2 = 4

2.2.
La fonction inverse est la fonction g(x) = 1/x

g(0,1) = 1/0,1 = 10
g(1) = 1/1 = 1
g(10) = 1/10 = 0,1

Taux de variation de la fonction inverse entre 0,1 et 1
(g(1) - g(0,1))/(1 - 0,1) = (1 - 10)/(1 - 0,1) = -9/0,9 = -10

Taux de variation de la fonction inverse entre 1 et 10
(g(10) - g(1))/(10 - 1) = (0,1 - 1)/(10 - 1) = -0,9/9 = -0,1

Population de Floirac

1.
La courbe croît le plus rapidement entre 1968 et 1975, donc c’est la période pendant laquelle l’évolution de la population est la plus rapide

2.
On modélise la population de Floirac par une fonction P telle que P(x) représente le nombre d’habitants pour l’année x.

P(1968) = 8241
P(1990) = 16384
P(2007) = 15794

Le taux de variation de la population de Floirac entre 1968 et 1990 est
(P(1990) - P(1968))/(1990 - 1968) = (16384 - 8241)/(1990 - 1968) = 8143/22 = 370 (à l’unité près)

Le taux de variation de la population de Floirac entre 1990 et 2007 est
(P(2007) - P(1990))/(2007 - 1990) = (15794 - 16384)/(2007 - 1990) = -590/17 = -35 (à l’unité près)

Conclusion
Le taux de variation entre 1968 et 1990 étant positif, la population de Floirac croît lors de cette période.
Le taux de variation entre 1990 et 2007 étant négatif, la population de Floirac décroît lors de cette période.

pour être sur les * c'est le signe "x" ?

Up

Oui le * c’est une multiplication et le / une division

OK merci

l'opax ça représente quoi ça "^" ?

Le 09 décembre 2023 à 23:59:09 :
l'opax ça représente quoi ça "^" ?

C'est la puissance

Le 10 décembre 2023 à 11:38:27 :

Le 09 décembre 2023 à 23:59:09 :
l'opax ça représente quoi ça "^" ?

C'est la puissance

ok

Le 10 décembre 2023 à 13:42:33 :
Tu peux m'expliquer ça ? Je comprends rien.

(je vais écrire vAB pour vecteur AB)

1.
D’après la relation de Chasles on a
vAC = vAB + vBC
vBD = vBA + vAD

Alors,
vAC.vBD = (vAB + vBC).(vBA + vAD)
En développant on obtient
vAC.vBD = vAB.vBA + vBC.vBA + vAB.vAD + vBC.vAD

On utilise la formule du produit scalaire, ici on a 3 cas :
- Les vecteurs sont colinéaires (parallèles) et de même sens : produit des longueurs
- Les vecteurs sont colinéaires (parallèles) et de sens opposés : produit des longueurs multiplié par -1
- Les vecteurs sont orthogonaux (forment un angle droit) : le produit scalaire est nul

Étant donné que le côté AB est la hauteur du trapèze rectangle ABCD on en déduit que les angles ABC et DAB sont les angles droits de ce trapèze.

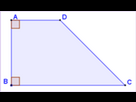
vAB et vBA sont colinéaires et de sens opposés
vAB.vBA = AB*BA*(-1) = 6*6*(-1) = -36

vBC et vBA sont orthogonaux
vBC.vBA = 0

vAB et vAD sont orthogonaux
vAB.vAD = 0

vBC et vAD sont colinéaires et de même sens
vBC.vAD = 9*4 = 36

Finalement
vAC.vBD = -36 + 0 + 0 + 36 = 0

2 .
Le produit scalaire de vAC et vBD vaut 0, ces vecteurs sont orthogonaux, donc les diagonales (AC) et (BD) sont perpendiculaires.

Debug

Le 11 décembre 2023 à 17:06:50 :
Tu peux me faire mon dm de math experte stp

Exercice 1.

1.(a)
17a + 17b = 17*(a + b)
Donc 17 divise 17a + 17b

1.(b)
7 divise 12a + 5b, alors il existe un entier k tel que 12a + 5b = 17k
5a + 12b = 17a + 17b - (12a + 5b) = 17a + 17b - 17k = 17*(a + b - k)
Donc 17 divise 5a + 12b

2.(a)
Supposons que 5n - 1 est divisible par 5
5 divise 5n
=> 5 divise -1 (absurde)
Donc 5n - 1 n’est pas divisible par 5

2.(b)
d divise 5n - 1
=> d divise 3*(5n - 1) = 15n - 3
d divise 15n + 8
=> d divise 15n + 8 - 3*(5n - 1) = 15n + 8 - 15n - 3 = 5

2.(c)
Je pense qu’il y a une erreur dans l’énoncé
Si on prend n = 2, 15n + 24 = 30 + 24 = 54 et 5n - 1 = 10 - 1 = 9
Et 54/9 n’est pas irréductible car 54 = 9*6 (cette fraction vaut 6)

Je suppose qu’il faut plutôt montrer que pour tout entier n, (15n + 8)/(5n - 1) est irréductible.

Soit d un entier naturel non nul qui divise 15n + 8 et 5n - 1, d’après la question 2.(b) d divise 5, donc les valeurs possibles de d sont 1 et 5.
Or, d’après la question 2.(a) 5n - 1 n’est pas divisible par 5 donc d =/= 5
=> d = 1
Donc la fraction est irréductible.

3.
On applique l’algorithme d’Euclide pour vérifier si 192 et 25 sont premiers entre eux
192 = 25*7 + 17
25 = 17*1 + 8
17 = 8*2 + 1
8 = 1*8 + 0
Le dernier reste non nul est 1, donc PGCD(192, 25) = 1
=> 192 et 25 sont premiers entre eux

D’après le théorème de Bézout il existe au moins un couple d’entiers solution de cette équation.

On cherche une solution particulière (x0, y0)
On remonte l’algorithme d’Euclide
1 = 17 - 2*8
1 = 17 - 2*(25 - 17)
1 = 192 - 25*7 - 2*(25 - 17*1)
1 = 192 - 25*7 - 2*(25 - (192 - 25*7))
1 = 192 - 7*25 - 2*25 + 2*192 - 2*7*25
1 = (1+2)*192 + (-7 - 2 - 2*7)*25
1 = 3*192 + (-23)*25
(x0, y0) = (3, -23) est une solution particulière de l’équation

Soit le couple d’entiers (x, y) solution de l’équation
192x + 25y = 192x0 + 25y0 = 1
=> 192x + 25y - (192x0 + 25y0) = 0
=> 192(x - x0) + 25(y - y0) = 0
=> 192(x - x0) = -25(y - y0)
=> 192(x - x0) = 25(y0 - y)

192 et 25 sont premiers entre eux, donc d’après le théorème de Gauss
192 divise y0 - y
=> il existe un entier naturel k tel que y0 - y = 192k
=> y = y0 - 192k = -23 - 192k
192x + 25y = 1
=> 192x = 1 - 25y
=> 192x = 1 - 25*(-23 - 192k)
=> 192x = 1 + 25*23 + 25*192k
=> 192x = 576 + 25*192k
=> 192x = 192*(3 + 25k)
=> x = 3 + 25k

Les solutions de cette équation sont les couples de la forme (3 + 25k, -23 - 192k) avec k un entier relatif

Exercice 2.

1.
Reste des divisions euclidiennes en fonction de n
n = 0 : 10^0 = 1 = 11*0 + 1 => reste = 1
n = 1 : 10^1 = 10 = 11*0 + 10 => reste = 10
n = 2 : 10^2 = 100 = 11*9 + 1 => reste = 1
n = 3 : 10^3 = 1000 = 11*90 + 10 => reste = 10
n = 4 : 10^4 = 10000 = 11*909 + 1 => reste = 1
n = 5 : 10^5 = 100000 = 11*9090 + 10 => reste = 10

On peut conjecturer que le reste de la division euclidienne de 10^n par 11 est 1 si n est pair ou 10 si n est impair.

On va démontrer cette conjecture par récurrence

- Initialisation : n = 0 pair
10^0 = 1 = 11*0 + 1 => reste = 1
La conjecture est vraie au premier rang

- Hérédité :
Supposons que la conjecture soit vraie pour un entier naturel n
Cas 1 : n est pair
Il existe un entier naturel q tel que 10^n = 11*q + 1
=> 10^(n+1) = (11*q + 1)*10
=> 10^(n+1) = 11*10q + 10
=> reste = 10 avec n + 1 impair
Cas 2 : n est impair
Il existe un entier naturel q tel que 10^n = 11*q + 10
=> 10^(n+1) = (11*q + 10)*10
=> 10^(n+1) = 11*10q + 100
=> 10^(n+1) = 11*10q + 11*9 + 1
=> 10^(n+1) = 11*(10q + 9) + 1
=> reste = 1 avec n + 1 pair

- Conclusion :
Pour tout entier naturel n, la conjecture est vérifiée

2.
On étudie les nombres de la forme
(n + 1)*10^3 + n*10^2 + (n + 2)*10^1 + (n + 3)*10^0
Avec n un entier naturel inférieur ou égal à 6

D’après la question 1.
(n + 1)*10^3 = (n + 1)*(11*q1 + 10) = (n + 1)*11*q1 + (n + 1)*10
n*10^2 = n*(11*q2 + 1) = n*11*q2 + n
(n + 2)*10^1 = (n + 2)*(11*q3 + 10) = (n + 2)*11*q3 + (n + 2)*10
(n + 3)*10^0 = (n + 3)*(11*q4 + 1) = (n + 3)*11*q4 + n + 3
avec q1, q2, q3 et q4 des entiers naturels

(n + 1)*10 + n + (n + 2)*10 + n + 3 = 10n + 10 + n + 10n + 20 + n + 3 = 22n + 33 = 11*(2n + 3)

Alors,
(n + 1)*10^3 + n*10^2 + (n + 2)*10^1 + (n + 3)*10^0 = 11*((n + 1)*q1 + n*q2 + (n + 2)*q3 + (n + 3)*q4) + (2n + 3))

Donc les nombres de cette forme sont divisibles pas 11

Exercice 3.

1.
p/q est une fraction irréductible
Donc PGCD(p, q) = 1

2.
racine(3) = p/q
=> 3 = (p/q)^2 = p^2/q^2
=> p^2 = 3q^2

3.
p congru à 0 mod 5
=> p^2 congru à 0^2 = 0 mod 5
p congru à 1 mod 5
=> p^2 congru à 1^2 = 1 mod 5
p congru à 2 mod 5
=> p^2 congru à 2^2 = 4 mod 5
p congru à 3 mod 5
=> p^2 congru à 3^2 = 9 mod 5
=> p^2 congru à 4 mod 5
p congru à 4 mod 5
=> p^2 congru à 4^2 = 16 mod 5
=> p^2 congru à 1 mod 5

4.
q congru à 0 mod 5
=> 3q^2 congru à 3*0^2 = 0 mod 5
q congru à 1 mod 5
=> 3q^2 congru à 3*1^2 = 3 mod 5
q congru à 2 mod 5
=> 3q^2 congru à 3*2^2 = 12 mod 5
=> 3q^2 congru à 2 mod 5
q congru à 3 mod 5
=> 3q^2 congru à 3*3^2 = 27 mod 5
=> 3q^2 congru à 2 mod 5
q congru à 4 mod 5
=> 3q^2 congru à 3*4^2 = 48 mod 5
=> 3q^2 congru à 3 mod 5

5.
p^2 = 3q^2
=> p^2 congru à 3q^2 mod 5
=> p^2 congru à 0 mod 5 et 3q^2 congru à 0 mod 5
=> p congru à 0 mod 5 et q congru à 0 mod 5
=> il existe deux entiers relatifs k, k’ tq p = 5k et q = 5k’
=> 5 divise p et 5 divise q
=> p/q n’est pas irréductible

Contradiction avec l’hypothèse de départ, donc racine(3) est irrationnel

J'aimerais avoir ton niveau en maths, comment t'as fais ?

PS : J'ai eu 5/5, je t'en suis infinimenr reconnaissant !

Le 12 décembre 2023 à 11:46:51 :
J'aimerais avoir ton niveau en maths, comment t'as fais ?

PS : J'ai eu 5/5, je t'en suis infinimenr reconnaissant !

Il faut faire des exercices régulièrement, c'est comme ça que tu travailles les notions et que tu les comprends/assimiles.
Chercher de la documentation autre que le cours de ton prof, parfois on comprend mieux une notion lorsqu'elle est expliquée avec une approche différente, aujourd'hui grâce à Internet il y a énormément de contenu gratuit donc c'est facile de trouver des cours/exos avec explications sur Youtube ou des sites de maths.

Salut l'OP, j'ai un exo à résoudre.
Montrez que si sum a_n z^n à pour rayon de convergence R>0, alors a_n (z^n)/n! converge sur C.

Mon idée: soit z dans C. On peut ecrire z = z'*k avec z' dans le disque de convergence et k réel.
La suite k^n/n! tends vers 0, donc elle est majorée par M.
On a donc sum a_n z^n/n! < M* sum a_n z'^n
Mais je vois pas comment conclure

Le 13 décembre 2023 à 20:18:53 :
Salut l'OP, j'ai un exo à résoudre.
Montrez que si sum a_n z^n à pour rayon de convergence R>0, alors a_n (z^n)/n! converge sur C.

Mon idée: soit z dans C. On peut ecrire z = z'*k avec z' dans le disque de convergence et k réel.
La suite k^n/n! tends vers 0, donc elle est majorée par M.
On a donc sum a_n z^n/n! < M* sum a_n z'^n
Mais je vois pas comment conclure

(abs(a) = valeur absolue de a)

Soit r un réel tel que 0 < r < R
sum an*r^n converge => la suite (an*r^n) est bornée

Soit M un majorant de (an*r^n)
abs(an*r^n)/n! = abs(an)*r^n*(1/n!) <= M*(1/n!)

Soit z un complexe, comme r =/= 0 on peut écrire abs(an*z^n) = abs(an)*abs(z^n) = abs(an)*abs(z^n)*r^n/r^n = abs(an)*r^n*(abs(z)/r)^n

abs(an*z^n/n!) = abs(an*z^n)/n! = abs(an)*r^n*(abs(z)/r)^n*(1/n!) <= M*(abs(z)/r)^n*(1/n!)

Alors,
sum (an*z^n/n!) <= M*sum (abs(z)/r)^n*(1/n!) = M*exp(abs(z)/r)

La série entière sum an*z^n/n! converge absolument sur C donc elle converge sur C

Salut, c'est juste pour demander de m'expliquer un truc que j'ai pas compris sur les produits scalaires avec la relation de Chasles, étant donné que t'as l'air de t'y connaitre.
Est-ce que si on prend par exemple BD.AC (sachant que BC fait, on va dire 4, et CD, 6) , est-ce (BC + CD).AC =
(4+6).AC ?
Bien sûr je garde à l'esprit que les termes distribués ne doivent pas être orthogonaux.
Merci d'avance !

@reyoudenoel14

Je note vAB pour vecteur AB
Je note AB pour longueur AB

Ce que tu dois retenir :
Le produit scalaire vAB.vCD est égal à
AB*CD*cos(angle(vAB,vCD))
Donc il y a 3 mesures à prendre en compte, la longueur AB, la longueur CD et l’angle formé par les vecteurs vAB et vCD qu’on a noté angle(vAB,vCD)

Il y a 3 cas particuliers qui facilitent les calculs :
- Si vAB et vCD sont colinéaires (parallèles) et ont le même sens alors l’angle formé par les vecteurs vAB et vCD est égal à 0° et cos(0) = 1 donc le produit scalaire vAB.vCD = AB*CD
- Si vAB et vCD sont colinéaires (parallèles) et ont un sens opposé alors l’angle formé par les vecteurs vAB et vCD est égal à 180° et cos(180) = -1 donc le produit scalaire vAB.vCD = -AB*CD
- Si vAB et vCD sont orthogonaux (les vecteurs forment un angle droit) alors l’angle formé par les vecteurs vAB et vCD est égal à 90° et cos(90) = 0 donc le produit scalaire vAB.vCD = 0

Pour revenir à ton exemple

Est-ce que si on prend par exemple BD.AC (sachant que BC fait, on va dire 4, et CD, 6) , est-ce (BC + CD).AC =
(4+6).AC ?

Il faut déjà bien faire la distinction entre le produit scalaire et la multiplication, car tu n’as pas le droit de faire un produit scalaire entre un nombre et un vecteur donc il faudrait plutôt écrire ici
(vBC + vCD).vAC = (BC+CD)*AC

Et cette égalité n’est pas toujours vraie, elle dépend de l’angle formé par les vecteurs vBC et vAC et de l’angle formé par les vecteurs vCD et vAC
Par exemple, si vAC est colinéaire à vBC et vCD mais de sens opposé à ces vecteurs alors
(vBC + vCD).vAC = vBC.vAC + vCD.vAC = -BC*AC - CD*AC = -(BC + CD)*AC
Elle est vraie si vAC est colinéaire aux vecteurs vBC et vCD et de même sens car on aurait
(vBC + vCD).vAC = vBC.vAC + vCD.vAC = BC*AC + CD*AC = (BC + CD)*AC

Le 16 décembre 2023 à 13:17:24 :
@reyoudenoel14

Je note vAB pour vecteur AB
Je note AB pour longueur AB

Ce que tu dois retenir :
Le produit scalaire vAB.vCD est égal à
AB*CD*cos(angle(vAB,vCD))
Donc il y a 3 mesures à prendre en compte, la longueur AB, la longueur CD et l’angle formé par les vecteurs vAB et vCD qu’on a noté angle(vAB,vCD)

Il y a 3 cas particuliers qui facilitent les calculs :
- Si vAB et vCD sont colinéaires (parallèles) et ont le même sens alors l’angle formé par les vecteurs vAB et vCD est égal à 0° et cos(0) = 1 donc le produit scalaire vAB.vCD = AB*CD
- Si vAB et vCD sont colinéaires (parallèles) et ont un sens opposé alors l’angle formé par les vecteurs vAB et vCD est égal à 180° et cos(180) = -1 donc le produit scalaire vAB.vCD = -AB*CD
- Si vAB et vCD sont orthogonaux (les vecteurs forment un angle droit) alors l’angle formé par les vecteurs vAB et vCD est égal à 90° et cos(90) = 0 donc le produit scalaire vAB.vCD = 0

Pour revenir à ton exemple

Est-ce que si on prend par exemple BD.AC (sachant que BC fait, on va dire 4, et CD, 6) , est-ce (BC + CD).AC =
(4+6).AC ?

Il faut déjà bien faire la distinction entre le produit scalaire et la multiplication, car tu n’as pas le droit de faire un produit scalaire entre un nombre et un vecteur donc il faudrait plutôt écrire ici
(vBC + vCD).vAC = (BC+CD)*AC

Et cette égalité n’est pas toujours vraie, elle dépend de l’angle formé par les vecteurs vBC et vAC et de l’angle formé par les vecteurs vCD et vAC
Par exemple, si vAC est colinéaire à vBC et vCD mais de sens opposé à ces vecteurs alors
(vBC + vCD).vAC = vBC.vAC + vCD.vAC = -BC*AC - CD*AC = -(BC + CD)*AC
Elle est vraie si vAC est colinéaire aux vecteurs vBC et vCD et de même sens car on aurait
(vBC + vCD).vAC = vBC.vAC + vCD.vAC = BC*AC + CD*AC = (BC + CD)*AC

Merci, je comprends mieux !