Le 16 février 2024 à 23:50:04 :
Merci beaucoup, cependant j'ai du mal à comprendre la formule : P a (B) = P(a) pour l'indépendance, tu pourrais clarifier ?

A et B sont indépendants si et seulement P(AnB) = P(A)*P(B)

La formule de la probabilité que l’événement A se réalise sachant que B est réalisé est
P(A | B) = P(AnB)/P(B)

Donc A et B sont indépendants
<=> P(A | B) = P(AnB)/P(B)
<=> P(A | B) = (P(A)*P(B))/P(B)
<=> P(A | B) = P(A)

L’événement B est indépendant de l’événement A si sa réalisation ou non n’influence pas celle de l’événement A (et inversement)
C’est pour ça que P(A | B) = P(A) et P(B | A) = P(B), un événement n’impacte pas la probabilité de l’autre événement

P(F) c'est pas 1450/2500 ?

Le 17 février 2024 à 00:46:44 :

Le 16 février 2024 à 23:50:04 :
Merci beaucoup, cependant j'ai du mal à comprendre la formule : P a (B) = P(a) pour l'indépendance, tu pourrais clarifier ?

A et B sont indépendants si et seulement P(AnB) = P(A)*P(B)

La formule de la probabilité que l’événement A se réalise sachant que B est réalisé est
P(A | B) = P(AnB)/P(B)

Donc A et B sont indépendants
<=> P(A | B) = P(AnB)/P(B)
<=> P(A | B) = (P(A)*P(B))/P(B)
<=> P(A | B) = P(A)

L’événement B est indépendant de l’événement A si sa réalisation ou non n’influence pas celle de l’événement A (et inversement)
C’est pour ça que P(A | B) = P(A) et P(B | A) = P(B), un événement n’impacte pas la probabilité de l’autre événement

Ah d'accord, je comprends mieux, merci !

Le 17 février 2024 à 01:21:27 :
P(F) c'est pas 1450/2500 ?

Effectivement j'ai fait une erreur, de même pour P(H), je rectifie

1.a.
P(F) = 272/2500
P(C) = 100/2500
P(FnC) = 58/2500

P(F) = 1450/2500

1.b.
P(F)*P(C) = (272/2500)*(100/2500) = (272*100)/(2500*2500) = 27200/6250000 = 0,004 à 10^-3 près

P(F)*P(C) = (1450/2500)*(100/2500) = 145000/6250000 = 58/2500 = P(FnC)

Donc F et C ne sont pas indépendants.

Donc F et C sont indépendants

2.a.
On note respectivement H et A les évènements « la personne est un homme » et « la personne ne pratique aucune de deux activités »

P(H) = 378/2500
P(A) = 1750/2500
P(HnA) = 630/2500

P(H I A) = P(HnA)/P(A) = (630/2500)/(1750/2500) = (630*2500)/(2500*1750) = 630/1750

P(H) = 1050/2500

2.b.
P(H) = 378/2500 = 0,1 à 10^-1 près
P(H I A) = 630/1750 = 0,4 à 10^-1 près

P(H) = 1050/2500 = (1050*1750)/(2500*1750) = 1837500/4375000
P(H I A) = 630/1750 = (630*2500)/(1750*2500) = 1732500/4375000

P(H) =/= P(H I A)
Donc H et A ne sont pas indépendants.

Le 17 février 2024 à 20:24:23 :

1.
AB = racine((-1 - (-2))² + (4 - (-3))²) = racine(1² + 7²) = racine(1 + 49) = racine(50) = racine(25*2) = racine(25)*racine(2) = 5*racine(2)

2.
On note C le milieu du segment [AB]

C = ((-2 + (-1))/2 ;(-3 + 4)/2)) = (-3/2 ;1/2)

3.
Soit M un point du plan.

vMA.vMB = 0
<=> (vMC + vCA).(vMC + vCB) = 0 (relation de Chasles)
<=> (vMC + vCA).(vMC + vAC) = 0 (vCB = vAC car C est le milieu de [AC])
<=> (vMC + vCA).(vMC - vCA) = 0 (vAC = -vCA)
<=> vMC² - vCA² = 0 (identité remarquable (a - b)*(a + b) = a² - b²)
<=> vMC² = vCA²
<=> ||vMC²|| = ||vCA²|| (passage à la norme des deux côtés)
<=> ||vMC||² = ||vCA||² (propriété de la norme)
<=> MC² = CA²
<=> MC = CA (passage par la racine carrée, on conserve l’égalité car ce sont des longueurs et donc elles sont positives)
<=> M est un point situé à une distance CA du milieu C du segment AB
<=> M est un point du cercle de centre C et de rayon AC

L’ensemble des points M du plan vérifiant vMA.vMB = 0 est le cercle de centre C et de rayon AC

Le 18 février 2024 à 00:46:27 :

Le 17 février 2024 à 20:24:23 :

1.
AB = racine((-1 - (-2))² + (4 - (-3))²) = racine(1² + 7²) = racine(1 + 49) = racine(50) = racine(25*2) = racine(25)*racine(2) = 5*racine(2)

2.
On note C le milieu du segment [AB]

C = ((-2 + (-1))/2 ;(-3 + 4)/2)) = (-3/2 ;1/2)

3.
Soit M un point du plan.

vMA.vMB = 0
<=> (vMC + vCA).(vMC + vCB) = 0 (relation de Chasles)
<=> (vMC + vCA).(vMC + vAC) = 0 (vCB = vAC car C est le milieu de [AC])
<=> (vMC + vCA).(vMC - vCA) = 0 (vAC = -vCA)
<=> vMC² - vCA² = 0 (identité remarquable (a - b)*(a + b) = a² - b²)
<=> vMC² = vCA²
<=> ||vMC²|| = ||vCA²|| (passage à la norme des deux côtés)
<=> ||vMC||² = ||vCA||² (propriété de la norme)
<=> MC² = CA²
<=> MC = CA (passage par la racine carrée, on conserve l’égalité car ce sont des longueurs et donc elles sont positives)
<=> M est un point situé à une distance CA du milieu C du segment AB
<=> M est un point du cercle de centre C et de rayon AC

L’ensemble des points M du plan vérifiant vMA.vMB = 0 est le cercle de centre C et de rayon AC

Merci, mais mais dans la question 2, c'est pas plutôt (4+3)/2 ?
Merci sinon !

Le 18 février 2024 à 00:57:20 :

Le 18 février 2024 à 00:46:27 :

Le 17 février 2024 à 20:24:23 :

1.
AB = racine((-1 - (-2))² + (4 - (-3))²) = racine(1² + 7²) = racine(1 + 49) = racine(50) = racine(25*2) = racine(25)*racine(2) = 5*racine(2)

2.
On note C le milieu du segment [AB]

C = ((-2 + (-1))/2 ;(-3 + 4)/2)) = (-3/2 ;1/2)

3.
Soit M un point du plan.

vMA.vMB = 0
<=> (vMC + vCA).(vMC + vCB) = 0 (relation de Chasles)
<=> (vMC + vCA).(vMC + vAC) = 0 (vCB = vAC car C est le milieu de [AC])
<=> (vMC + vCA).(vMC - vCA) = 0 (vAC = -vCA)
<=> vMC² - vCA² = 0 (identité remarquable (a - b)*(a + b) = a² - b²)
<=> vMC² = vCA²
<=> ||vMC²|| = ||vCA²|| (passage à la norme des deux côtés)
<=> ||vMC||² = ||vCA||² (propriété de la norme)
<=> MC² = CA²
<=> MC = CA (passage par la racine carrée, on conserve l’égalité car ce sont des longueurs et donc elles sont positives)
<=> M est un point situé à une distance CA du milieu C du segment AB
<=> M est un point du cercle de centre C et de rayon AC

L’ensemble des points M du plan vérifiant vMA.vMB = 0 est le cercle de centre C et de rayon AC

Merci, mais mais dans la question 2, c'est pas plutôt (4+3)/2 ?
Merci sinon !

On a A(xA;yA) et B(xB;yB) deux points du plan

Le milieu du segment [AB] est le point qui a pour coordonnées
((xA + xB)/2;(yA + yB)/2)

Ici yA = -3 et yB = 4 donc on a bien pour ordonnée (-3 + 4)/2 = 1/2

Exercice 1/2:
Résoudre dans R(éel) l'équation (ignore les petit points de suspension)
7-2x . . . 4x+1 . . . . . . . 4
_____ + _______ =_____________
x-3 . . . . . x+1 . . . . . (x-3)(x+1)
Exercice 2/2:
Le directeur marketing d'une chaîne d'ameublement decide refaire toutes les entrées des magasins de la chaîne selon le schéma ci dessous:
Le rectangle ABCD représente une grande porte de largeur 160cm et de hauteur 240cm. O et E sont les milieux respectifs de [AD] et [BC]. Cette porte est encadrée par deux panneaux obliques qui touchent les montants haut-gauche (C) et haut-droit (B) de la porte afin de représenter un «A» stylisé. On appelle x la largeur au sol entre un panneau oblique et le montant le plus proche de la porte: AG = DF = x.
1. À quel intervalle appartient x ?
2. a. Justifier que:
240 . . . . x
____ = _______
HO . . . x+80
b. en déduire que:
. . . . . . . . . . .19200
HO = 240 - _________
. . . . . . . . . . . . x
3. Le directeur souhaite que les deux panneaux obliques se rejoignent à quatre mètres de hauteur. Quelle sera la distance au sol entre ces deux panneaux ?

Le 04 mars 2024 à 07:46:09 :
Exercice 1/2:
Résoudre dans R(éel) l'équation (ignore les petit points de suspension)
7-2x . . . 4x+1 . . . . . . . 4
_____ + _______ =_____________
x-3 . . . . . x+1 . . . . . (x-3)(x+1)
Exercice 2/2:
Le directeur marketing d'une chaîne d'ameublement decide refaire toutes les entrées des magasins de la chaîne selon le schéma ci dessous:
Le rectangle ABCD représente une grande porte de largeur 160cm et de hauteur 240cm. O et E sont les milieux respectifs de [AD] et [BC]. Cette porte est encadrée par deux panneaux obliques qui touchent les montants haut-gauche (C) et haut-droit (B) de la porte afin de représenter un «A» stylisé. On appelle x la largeur au sol entre un panneau oblique et le montant le plus proche de la porte: AG = DF = x.
1. À quel intervalle appartient x ?
2. a. Justifier que:
240 . . . . x
____ = _______
HO . . . x+80
b. en déduire que:
. . . . . . . . . . .19200
HO = 240 - _________
. . . . . . . . . . . . x
3. Le directeur souhaite que les deux panneaux obliques se rejoignent à quatre mètres de hauteur. Quelle sera la distance au sol entre ces deux panneaux ?

Exercice 1/2

On suppose que x =/= 1 et x =/= 3

(7 - 2x)/(x - 3) + (4x + 1)/(x + 1) = 4/((x - 3)(x + 1))
<=> (7 - 2x)(x + 1) + (4x + 1)(x - 3) - 4 = 0
<=> 7x + 7 - 2x² - 2x + 4x² + x - 12x - 3 - 4 = 0
<=> 2x² - 6x = 0
<=> x(2x - 6) = 0
<=> x = 0 (car x =/= 3)

S = {0}

Exercice 2/2

1.
x est dans l’intervalle [0 ; +inf[

2.a.
On s’intéresse au triangle HGO
Les points GBH sont alignés
Les points GAO sont alignés
(HO) et (BA) sont parallèles
Donc d’après le théorème de Thalès
AB/HO = GA/GO
<=> 240/HO = x/(x + 80)

2.b. (erreur dans l’énoncé, c’est un + à la place du -, HO = 240 + 19200/x)
240/HO = x/(x + 80)
<=> HO/240 = (x + 80)/x
<=> HO/240 = 1 + 80/x
<=> HO = 240 + 19200/x

3.
HO = 400
<=> 400 = 240 + 19200/x
<=> 160 = 19200/x
<=> 1/160 = x/19200
<=> x = 19200/160
<=> x = 120 cm

FG = 2x + 160
<=> FG = 2*120 + 160
<=> FG = 400 cm

Le 22 mars 2024 à 22:01:58 :

1.

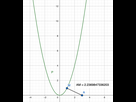
Avec GeoGebra on observe que la longueur AM est minimum lorsque l’abscisse du point M est proche de 1 et que cette longueur vaut environ 2,24 à 10^-2 près.

2.
AM étant une distance elle est positive. Comme la fonction carré est croissante sur les valeurs réelles positives, AM est minimale si et seulement si AM² est minimale.

3.a.
Le point M a pour coordonnées (x ; x²)
On peut alors calculer la distance AM
AM = racine((x - 3)² + (x² - 0)²) = racine(x² - 6x + 9 + x^4)
Par conséquent, AM² = x^4 + x² - 6x + 9
Donc d(x) = x^4 + x² - 6x + 9

3.b.
d’(x) = 4x^3 + 2x - 6

d’(1) = 4 + 2 - 6 = 0
1 est racine de d’, donc il existe des réels a, b et c qui vérifient d’(x) = (x - 1)(ax² + bx + c)

En développant on obtient
d’(x) = (x - 1)(ax² + bx + c) = ax^3 + bx² + cx - ax² - bx - c = ax^3 + (b - a)x² + (c - b)x - c = 4x^3 + 2x - 6
Par identification, on a
a = 4
b - a = 0
c - b = 2
-c = -6
<=>
a = 4
b = 4
c = 6

Donc d’(x) = (x - 1)(4x² + 4x + 6)

3.c.
On étudie le signe de d’(x) = (x - 1)(4x² + 4x + 6)
On a un produit, donc on étudie le signe des deux facteurs :

- Étude du signe de x - 1 :
x - 1 > 0 <=> x > 1
Et x - 1 s’annule en 1

- Étude du signe de 4x² + 4x + 6
On a un polynôme de degré 2, on calcule le discriminant de ce polynôme
Delta = 4² - 4*4*6 = 16 - 96 = -80 < 0
Ce polynôme n’a pas de racine réelle, son coefficient dominant est 4 > 0, par conséquent, il est strictement positif sur [0 ; +inf[

d(0) = 9
d(1) = 5

On a donc le tableau de variations complet de d sur [0 ; +inf[

4.
D’après l’étude faite à la question 3. la fonction d atteint son minimum en x = 1 et vaut 5
Donc AM = racine(5) = 2,24 à 10^-2 près

Le 23 mars 2024 à 09:16:17 :

1. VRAI
La courbe C’ est en dessous de l’axe des abscisses sur [-3 ; -1], par conséquent, f’(x) <= 0 sur cet intervalle.

2. VRAI
La courbe C’ est au dessus de l’axe des abscisses sur [-1 ; 2], par conséquent, f’(x) >= 0 sur cet intervalle, donc f est croissante sur cet intervalle.

3. FAUX
D’après le graphique, f’(-3) < -1

4. VRAI
La tangente à la courbe C au point d’abscisse 0 a pour équation
y = f’(0)(x - 0) + f(0)
D’après l’énoncé, f(0) = -1
D’après le graphique f’(0) = 1
y = x - 1

Au point d’abscisse 1, cette tangente a pour ordonnée 1 - 1 = 0
Donc la tangente à la courbe C au point d’abscisse 0 passe par le point de coordonnées (1 ; 0)

15 - 18 c'est lycée pas collège

Merci d'avance clé

Le 18 avril 2024 à 23:24:59 :

Merci d'avance clé

1.
Solution générale de l’équation y’ = alpha*y
yc(x) = C*exp(alpha*x) avec C une constante réelle.

Solution particulière de (E)
p(x) = -(-22*alpha)/alpha = 22

Solution générale de (E)
thetac(x) = yc(x) + p(x) = C*exp(alpha*x) + 22 avec C une constante réelle

2.
theta’(t) = alpha(theta(t) - 22) = alpha*theta(t) - alpha*22
Donc theta est une solution de (E), ce qui veut dire qu’elle est sous la forme
theta(t) = C*exp(alpha*t) + 22 avec C une constante réelle
On détermine C grâce à la condition initiale de l’énoncé.
Au moment de sortir la tarte du four, sa température est de 180°C => theta(0) = 180
theta(0) = C*exp(alpha*0) + 22 = C*exp(0) + 22 = C + 22
<=> 180 = C + 22
<=> C = 158
Donc theta(t) = 158*exp(alpha*t) + 22

3.
20 minutes après avoir sorti la tarte du four, sa température a diminué de 80°C => theta(20) = 180 - 80 = 100
theta(20) = 158*exp(alpha*20) + 22
<=> 100 = 158*exp(alpha*20) + 22
<=> (100 - 22)/158 = exp(alpha*20)
<=> 78/158 = exp(alpha*20)
<=> exp(20*alpha) = 39/79

4.a)
f’(x) = 20*exp(20x)
La fonction exponentielle est strictement positive sur R => f’ est strictement positive sur R => f est strictement croissante sur R
lim x->-inf f(x) = 0 et lim x->+inf f(x) = +inf
On en déduit donc le tableau de variation complet de f

4.b)
f est dérivable sur R donc continue sur R
f est strictement croissante sur R
39/79 est dans l’intervalle [lim x->-inf f(x) ; lim x->+inf f(x)[ = [0 ; +inf[
Donc d’après le corollaire du théorème des valeurs intermédiaires, il existe un unique alpha dans R qui soit solution de l’équation f(x) = 39/79

4.c)
exp(20*alpha) = 39/79
<=> ln(exp(20*alpha)) = ln(39/79)
<=> 20*alpha = ln(39/79)
<=> alpha = ln(39/79)/20
alpha = -0,0353 à 10^-4 près

5.a)
alpha < 0
=> lim t->+inf exp(alpha*t) = 0
=> lim t->+inf theta(t) = 22

5.b)
theta’(t) = alpha*(theta(t) - 22)
theta(t) - 22 = 158*exp(alpha*t) + 22 - 22 = 158*exp(alpha*t)
pour tout t dans [0 ; +inf[, theta(t) - 22 > 0
alpha < 0
=> pour tout t dans [0 ; +inf[, theta’(t) < 0
=> pour tout t dans [0 ; +inf[ theta(t) est strictement décroissante

5.c)
La tarte doit être servie idéalement à une température de 25°C
theta(t) = 25
<=> 158*exp(alpha*t) + 22 = 25
<=> exp(alpha*t) = (25 - 22)/158
<=> exp(alpha*t) = 3/158
<=> ln(exp(alpha*t)) = ln(3/158)
<=> alpha*t = ln(3/158)
<=> t = ln(3/158)/alpha
t = 112 à l’unité près
Justin devra attendre 112 minutes avant de déguster sa tarte.

J'ai tout mis mais c'est juste le dernier exo que je comprends rien avec le délire de "pose le changement de variable" je comprends pas

Le 19 avril 2024 à 10:46:33 :

J'ai tout mis mais c'est juste le dernier exo que je comprends rien avec le délire de "pose le changement de variable" je comprends pas

Exercice 4 :

1)
Sur Excel on obtient :

L’ajustement affine ne convient pas pour cette série car les point ne sont pas sensiblement alignés donc les écarts entre les points et la droite d’ajustement affine sont trop importants.

2)
Tu remplaces la ligne des xi de ton tableau par la ligne des zi = 1/xi (ex : la première colonne c’est z1 = 1/x1 = 1/3,68) ce qui te donne le tableau suivant avec les zi arrondis à 10^-3 près :

On obtient donc le nuage de points ainsi que la droite d’ajustement affine :

(Ici ils affichent l’équation de la droite en fonction de x, mais c’est bien en fonction de z)

Ce nouvel ajustement affine convient pour cette série, car les points sont sensiblement alignés donc les écarts entre les points et la droite d’ajustement affine sont bien plus acceptables.

3)
Une équation de la droite d’ajustement est y = 47,08z + 0,37 avec les coefficients arrondis à 10^-2 près.

4)
z = 1/x
Donc y = 47,08/x + 0,37

x = 54 kW, on remplace dans l’équation pour déterminer le temps en heures
y = 47,08/54 + 0,37 = 1,2 h à 10^-1 près

Si on convertit ce temps en minutes, ça nous donne 1,2*60 = 72 minutes donc 1h12min.

5)
y = 47,08/x + 0,37
=> y - 0,37 = 47,08/x
=> (y - 0,37)/47,08 = 1/x
=> x = 47,08/(y - 0,37)

Convertir 45min en heures : 45/60 = 0,75h

On remplace le temps y dans l’équation x = 47,08/(y - 0,37) pour trouver la puissance fournie x
x = 47,08/(0,75 - 0,37) = 123,895 kW à 10^-3 près

Le 19 avril 2024 à 14:38:32 :

Le 19 avril 2024 à 10:46:33 :

J'ai tout mis mais c'est juste le dernier exo que je comprends rien avec le délire de "pose le changement de variable" je comprends pas

Exercice 4 :

1)
Sur Excel on obtient :

L’ajustement affine ne convient pas pour cette série car les point ne sont pas sensiblement alignés donc les écarts entre les points et la droite d’ajustement affine sont trop importants.

2)
Tu remplaces la ligne des xi de ton tableau par la ligne des zi = 1/xi (ex : la première colonne c’est z1 = 1/x1 = 1/3,68) ce qui te donne le tableau suivant avec les zi arrondis à 10^-3 près :

On obtient donc le nuage de points ainsi que la droite d’ajustement affine :

(Ici ils affichent l’équation de la droite en fonction de x, mais c’est bien en fonction de z)

Ce nouvel ajustement affine convient pour cette série, car les points sont sensiblement alignés donc les écarts entre les points et la droite d’ajustement affine sont bien plus acceptables.

3)
Une équation de la droite d’ajustement est y = 47,08z + 0,37 avec les coefficients arrondis à 10^-2 près.

4)
z = 1/y
Donc y = 47,08/x + 0,37

x = 54 kW, on remplace dans l’équation pour déterminer le temps en heures
y = 47,08/54 + 0,37 = 1,2 h à 10^-1 près

Si on convertit ce temps en minutes, ça nous donne 1,2*60 = 72 minutes donc 1h12min.

5)
y = 47,08/x + 0,37
=> y - 0,37 = 47,08/x
=> (y - 0,37)/47,08 = 1/x
=> x = 47,08/(y - 0,37)

Convertir 45min en heures : 45/60 = 0,75h

On remplace le temps y dans l’équation x = 47,08/(y - 0,37) pour trouver la puissance fournie x
x = 47,08/(0,75 - 0,37) = 123,895 kW à 10^-3 près

Merci énormément khey