C'est bon le dm je l'ai finis j'avais trouvé exactement ce que tu m'as envoyé sur internet merci quand même Jakarta-Sch

Le 05 novembre 2023 à 11:09:04 :
Calculer la mesure de l'angle au centre IOM correspondant à la position du point M sur le cercle trigonométrique lorsque la mesure principale de l'angle orienté (OI, OM) est 1 radian ?

Âme charitable venez m'aider je vous en conjure.

180 degrés = pi radians
Donc pour une mesure en radian de 1 tu as une mesure en degrés de 180/pi = 57,29... degrés

Le 05 novembre 2023 à 10:19:21 :
C'est vraiment urgent les kheys je pige RIEN DU TOUT.
Comment je peux trouver un angle en radiant à partir d'un cosinus ? Comment je suis sensé calculer un sinus à partir du résultat COMMMENT putain ????
Merci d'avance aux âmes charitables qui voudront bien m'aider.

UP
J'ai à peu près réussi la partie cosinus, la partie sinus et les angles associés m'iront car je comprend rien, merci d'avance

Le 05 novembre 2023 à 15:04:20 :

Le 05 novembre 2023 à 10:19:21 :
C'est vraiment urgent les kheys je pige RIEN DU TOUT.
Comment je peux trouver un angle en radiant à partir d'un cosinus ? Comment je suis sensé calculer un sinus à partir du résultat COMMMENT putain ????
Merci d'avance aux âmes charitables qui voudront bien m'aider.

UP
J'ai à peu près réussi la partie cosinus, la partie sinus et les angles associés m'iront car je comprend rien, merci d'avance

Exercice 4 : Sinus

a.
Sur [-pi/2 ; 0] la fonction sinus est négative, donc sin(t) est négatif
sin^2(t) + cos^2(t) = 1
<=> sin^2(t) = 1 - cos^2(t)
<=> sin^2(t) = 1 - (1/3)^2
<=> sin^2(t) = 8/9
<=> sin(t) = racine(8/9) = racine(8)/racine(9) = racine(8)/3 (en valeur absolue)
Donc sin(t) = -racine(8)/3

b.
arcsin(racine(8)/3) = 1,23 à 10^-3 près qui se trouve dans ]0 ; pi/2]
On veut une valeur de t qui se trouve dans [-pi/2 ; 0], comme la fonction sinus est impaire et que -arcsin(racine(8)/3) se trouve dans l’intervalle [-pi/2 ; 0], on en déduit que t = -arcsin(racine(8)/3) = -1,231 à 10^-3 près.

Exercice 5 : Cosinus

a.
Sur [pi/2 ; pi] la fonction cosinus est négative ; donc cos(t) est négatif
cos^2(t) + sin^2(t) = 1
<=> cos(t) = racine(1 - sin^2(t)) = racine(1 - (1/4)^2) = racine(15/16) = racine(15)/4 (en valeur absolue)
Donc cos(t) = -racine(15)/4

b.
arccos(racine(15)/4) = 0,253 à 10^-3 près qui se trouve dans l’intervalle [0 ; pi/2[
On veut une valeur de t qui se trouve dans [pi/2 ; pi], comme pi - arccos(racine(15)/4) se trouve dans l’intervalle [pi/2 ; pi], avec la réflexion d’axe x = pi/2 de la fonction cosinus, on en déduit que t = pi - arccos(racine(15)/4) =2,889 à 10^-3 près.

Exercice 6 : Angles associés

sin(pi - t) = sin(t)
sin(t - 4pi) = sin(t)
sin(t + 3pi) = sin(t + pi) = -sin(t)
sin(pi/2 + t) = cos(t)
Donc A = sin(t) + sin(t) - sin(t) + cos(t) = cos(t) + sin(t)

cos(t + pi) = -cos(t)
cos(pi/2 - t) = sin(t)
cos(pi/2 + t) = -sin(t)
cos(7pi - t) = cos(pi - t) = -cos(t)
Donc B = -cos(t) + sin(t) - sin(t) - cos(t) = -2*cos(t)

Merci beaucoup ! Je saurais pas comment exprimer mon immense gratitude pour ton aide ! Je t'en remercie infiniment
Je te souhaite tous le bonheur du monde khey, merci encore, tu m'a sauvé !

Soit ABC un triangle rectangle en A et H le projeté orthogonale de A sur (BC). Soit D le point tel que ABDH est un parallélogramme et E le point tel que ACEH est un parallélogramme
1. Déterminer l'image de B par la translation t qui transforme A en H
2. Démontrer que BCED est un rectangle

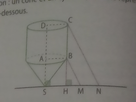
Deux échelles ont été posées contre le silo ((c'est le cylindre et le cône que tu vois sur la figure)) elles sont représentés sur la figurepar des segments [BM] et [CN]. On donne SM=2,1m et SN=3,3m. On note H le pied de la hauteur issue de B dans les triangle SBM. Les points S, H, M et Ne sont alignés Les points C, B et H sont alignés. Les deux échelles sont elles parallèles ? Justifier la réponse.

Le 05 novembre 2023 à 23:54:55 :
Soit ABC un triangle rectangle en A et H le projeté orthogonale de A sur (BC). Soit D le point tel que ABDH est un parallélogramme et E le point tel que ACEH est un parallélogramme
1. Déterminer l'image de B par la translation t qui transforme A en H
2. Démontrer que BCED est un rectangle

1.
L’image de B par la translation t est parallèle et de même longueur que [AH]
ABDH est un parallélogramme, donc [BD] est parallèle et de même longueur que [AH].
Par conséquent, l’image de B par la translation t est le point D

2.
ABDH est un parallélogramme, donc BD = AH et (BD) // (AH)
ACEH est un parallélogramme, donc AH = CE et (AH) // (CE)
Donc BD = CE et (BD) // (CE), BCED est un parallélogramme
H est le projeté orthogonale de A sur (BC), comme (AH) // (BD) et (BC) // (DE), D est le projeté orthogonal de B sur (DE), comme (BD) // (CE) E est le projeté orthogonal de C sur (DE).
Donc BCED est un parallélogramme avec des angles droits, c’est un rectangle.

Le 06 novembre 2023 à 00:35:45 :

Deux échelles ont été posées contre le silo ((c'est le cylindre et le cône que tu vois sur la figure)) elles sont représentés sur la figurepar des segments [BM] et [CN]. On donne SM=2,1m et SN=3,3m. On note H le pied de la hauteur issue de B dans les triangle SBM. Les points S, H, M et Ne sont alignés Les points C, B et H sont alignés. Les deux échelles sont elles parallèles ? Justifier la réponse.

Il manque des informations pour faire cet exo.
Comme les points H,M et N sont alignés et le points H,B et C sont alignés, si on montre qu'il y a égalité entre les rapports HB/HC et HM/HN alors [BM] et [CN] sont parallèles (réciproque du théorème de Thales).
Pour ça il faut calculer HB,HC, HM et HN, mais on ne peut pas le faire avec les infos que tu m'as donnés.

Punaise je suis dyscalculique j’ai l’impression de lire du CHINOIS

Le 06 novembre 2023 à 01:34:48 :

Le 06 novembre 2023 à 00:35:45 :

Deux échelles ont été posées contre le silo ((c'est le cylindre et le cône que tu vois sur la figure)) elles sont représentés sur la figurepar des segments [BM] et [CN]. On donne SM=2,1m et SN=3,3m. On note H le pied de la hauteur issue de B dans les triangle SBM. Les points S, H, M et Ne sont alignés Les points C, B et H sont alignés. Les deux échelles sont elles parallèles ? Justifier la réponse.

Il manque des informations pour faire cet exo.
Comme les points H,M et N sont alignés et le points H,B et C sont alignés, si on montre qu'il y a égalité entre les rapports HB/HC et HM/HN alors [BM] et [CN] sont parallèles (réciproque du théorème de Thales).
Pour ça il faut calculer HB,HC, HM et HN, mais on ne peut pas le faire avec les infos que tu m'as donnés.

Milles excuses !!! Je te donnes les infos tout de suite et merci beaucoup pour ce que ta fait tu sauve

Tout ce qu'il y a de marqué en plus c'est AS=1,60m; DA=2,40 et AB=1,30

Le 06 novembre 2023 à 01:34:48 :

Le 06 novembre 2023 à 00:35:45 :

Deux échelles ont été posées contre le silo ((c'est le cylindre et le cône que tu vois sur la figure)) elles sont représentés sur la figurepar des segments [BM] et [CN]. On donne SM=2,1m et SN=3,3m. On note H le pied de la hauteur issue de B dans les triangle SBM. Les points S, H, M et Ne sont alignés Les points C, B et H sont alignés. Les deux échelles sont elles parallèles ? Justifier la réponse.

Il manque des informations pour faire cet exo.
Comme les points H,M et N sont alignés et le points H,B et C sont alignés, si on montre qu'il y a égalité entre les rapports HB/HC et HM/HN alors [BM] et [CN] sont parallèles (réciproque du théorème de Thales).
Pour ça il faut calculer HB,HC, HM et HN, mais on ne peut pas le faire avec les infos que tu m'as donnés.

Le 06 novembre 2023 à 01:59:59 :
Tout ce qu'il y a de marqué en plus c'est AS=1,60m; DA=2,40 et AB=1,30

HN = SN - SH
SH = AB = 1,3 m
HN = 3,3 - 1,3 = 2 m
HM = SM - SH
HM = 2,1 - 1,3 = 0,8 m
HM/HN = 0,8/2 = 0,4

HC = SD
SD = SA + AD
SD = 1,6 + 2,4 = 4 m
HC = 4 m
HB = SA
HB = 1,6 m
HB/HC = 1,6/4 = 0,4

Alignements de H,M,N et H,B,C
HM/HN = HB/HC
Donc d'après la réciproque du théorème de Thales, (BM) et (CN) sont parallèles.
Donc les échelles sont parallèles

Le 06 novembre 2023 à 02:16:37 :

Le 06 novembre 2023 à 01:34:48 :

Le 06 novembre 2023 à 00:35:45 :

Deux échelles ont été posées contre le silo ((c'est le cylindre et le cône que tu vois sur la figure)) elles sont représentés sur la figurepar des segments [BM] et [CN]. On donne SM=2,1m et SN=3,3m. On note H le pied de la hauteur issue de B dans les triangle SBM. Les points S, H, M et Ne sont alignés Les points C, B et H sont alignés. Les deux échelles sont elles parallèles ? Justifier la réponse.

Il manque des informations pour faire cet exo.
Comme les points H,M et N sont alignés et le points H,B et C sont alignés, si on montre qu'il y a égalité entre les rapports HB/HC et HM/HN alors [BM] et [CN] sont parallèles (réciproque du théorème de Thales).
Pour ça il faut calculer HB,HC, HM et HN, mais on ne peut pas le faire avec les infos que tu m'as donnés.

HN = SN - SH
SH = AB = 1,3 m
HN = 3,3 - 1,3 = 2 m
HM = SM - SH
HM = 2,1 - 1,3 = 0,8 m
HM/HN = 0,8/2 = 0,4

HC = SD
SD = SA + AD
SD = 1,6 + 2,4 = 4 m
HC = 4 m
HB = SA
HB = 1,6 m
HB/HC = 1,6/4 = 0,4

Alignements de H,M,N et H,B,C
HM/HN = HB/HC
Donc d'après la réciproque du théorème de Thales, (BM) et (CN) sont parallèles.
Donc les échelles sont parallèles

Merci beaucoup c'est très gentil!

Le 14 novembre 2023 à 19:08:55 :
Salut frero tu pourrais maider sur un exercice de fonction que j’ai complètement raté dans mon ds dd Terminale spé math

1.
La tangente au point A(-1;9/2) est parallèle à l’axe des abscisses. Donc son coefficient directeur est nul
f’(-1) = 0

La tangente au point B(2;0) passe par le point (0;2)
On en déduit son coefficient directeur qui est (0-2)/(2-0) = -1
f’(2) = -1

2.
La tangente au point d’abscisse 1 passe par le point (1;f(1))
Donc f(1) = -2*1 + 7/2 = -4/2 + 7/2 = 3/2

La tangente au point d’abscisse 1, y = -2x... a -2 pour coefficient directeur
Donc f’(1) = -2

3.a) FAUX
f est strictement décroissante en 0 donc f’(0) < 0
f est strictement décroissante en 3 donc f’(3) < 0
Donc f’(0)*f’(3) > 0

3.b) VRAI
f est strictement croissante en -3 donc f’(-3) > 0
f est strictement décroissante sur en 1 donc f’(1) < 0
Donc f’(-3)*f’(1) < 0 (on peut aussi écrire f'(-3)*f'(1) <= 0)

Bonsoir j’ai un dm pour demain et je n’ai vrm rien compris (je suis en terminale spé maths), il serait possible de m’aider en m’expliquant la méthodologie clairement parce que j’ai vrm envie de comprendre

Le 14 novembre 2023 à 23:48:06 :

Bonsoir j’ai un dm pour demain et je n’ai vrm rien compris (je suis en terminale spé maths), il serait possible de m’aider en m’expliquant la méthodologie clairement parce que j’ai vrm envie de comprendre

1.
Pour étudier les variations de f, il faut étudier le signe de la dérivée f’
f’(x) = -2*exp(-x) - 2x + 2

Pour étudier le signe de cette dérivée, on va étudier les variations de cette dérivée, on dérive une deuxième fois, puis on étudie le signe de f’’
f’’(x) = 2*exp(-x) - 2 = 2*(exp(-x) - 1)

Le signe de f’’ est le signe de exp(-x) - 1
exp(-x) - 1 <= 0
<=> exp(-x) <= 1
<=> ln(exp(-x)) <= ln(1)
<=> -x <= 0
<=> x >= 0

f’’ est négative sur [0 ; +infini[ donc f’ est décroissante sur [0 ; +infini[
Il en découle que f’’ est positive sur ]-infini ; 0] donc f’ est croissante sur ]-infini ; 0]

f’(0) = -2*exp(0) - 2*0 + 2 = -2 + 2 = 0
Or, d’après les variations de f’, pour tout réel x, f’(x) <= f’(0) = 0

Conclusion f est décroissante sur R.

2.
On étudie le signe de f(x) - g(x)
On observe que f(x) = 2*exp(-x) + g(x)
Alors, f(x) - g(x) = 2*exp(-x)
La fonction exponentielle est positive sur R donc 2*exp(-x) >= 0 pour tout x dans R
f(x) - g(x) >= 0
<=> f(x) >= g(x)
La courbe de f est au dessus de la courbe de g sur R.

Salut comment cherché la dérivée de 3 racine de x ?

Le 16 novembre 2023 à 11:51:35 :
Salut comment cherché la dérivée de 3 racine de x ?

(3*racine(x))' = 3*(racine(x))' = 3/(2*racine(x))

Avec la formule de dérivé stp