prépare moi un cours sur les sommes doubles, si possible en m'expliquant le rapport avec les matrices
les produits avec le signe pi
les démonstrations par récurrence avec des inégalités style avec des factorielles
le principe de la récurrence forte..

fais ça vite

QUARANTE EUROS PAR HEURE

mec je te prends pr 35€

enfin je te prends en cours
heu

"les produits avec le signe pi "

ça c'est encore un problème non résolu, les plus grands mathématiciens du monde travaillent dessus

:ptsi:

tkt je me sens de taille

barack c'est bien toi qui es dans une ECS à je sais plus combien de milliers d'euros par an parce que soi disant les profs sont meilleurs ?

mec tu t'es monté le bourichon tout seul sur cette affaire, j'ai toujours été nuancé sur la question de la qualité de l'enseignement privé/public mais au final je ne suis pas dans une prépa full privé à 15k/an, je suis juste dans une semi privé donc ça reste un service non marchand sous contrat avec l'Etat, 1,9k/an

et j'ai juste la malchance d'être tombé sur le mauvais prof qui est neuf de cette année, on fait 2x moins de trucs que la classe d'à côté

ouais t'avais qu'à aller dans une vraie prépa (ie publique)

qui me rédige une démonstration par récurrence avec une inégalité et des factorielles svp ? oklm

c'est bien d'utiliser des termes mathématiques mais quand ils ont un sens mis bout à bout c'est mieux

pour tout n >= 1
k=1 sigma n de k! =< (n+1)!
j'sais pas pourquoi j'ai bloqué là dessus au dst, je me retrouvais à un truc en divisant les deux termes style somme de k! entre 1 et n + (n+1)! =< (n+1)! (n+2) et je savais pas aller plus loin

:ecs:

nan j'suis en ece

SPLIT

j'avais jamais vu tous ces trucs au lycée justement

bah par récurrence c'est izi
cas de base trivial
après tu supposes que c'est vrai à n
(n+2) ! = (n+2)*(n+1)!
tu sors le (n+1) ! de ta somme avec k et t'as plus qu'à prouver que (n+1) ! < (n+1)*(n+1)! ce qui est trivial
tu sommes les 2 inégalités
bim bam boum la chatte à mcdoom

ah mais oui crayonsikea je croyais que t'avais fait une faute dans ton truc et je comprenais toujours rien et en le ré-écrivant sur paint j'ai fait un truc et je crois que c'est ce que t'as expliqué mais je suis pas sûr, c'est ça que tu voulais dire ?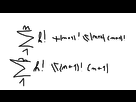

donc on soustrait par (n+1)!, puis on factorise par (n+1)! à droite puis par hypothèse de récurrence et le fait que n soit supérieur à 1 l'inégalité est démontrée c sa ?

je sais pas si c'est ça parce que je comprends pas le "tu sommes les deux inégalités"

bah tu soustrais juste (n+1)! de chaque côté en faite…