Page issue de la soluce de Professeur Layton et l'Étrange Village.
Maison de la décoratrice
Trouvez les 30 objets à répartir dans les chambres de Layton et Luke et placez-les correctement pour débloquer ces trois énigmes bonus.
Enigme 124 : Marée haute (50 picarats)
Une échelle de corde, suspendue au flanc d'un navire, est peu à peu submergée par la marée. Au départ, l'eau arrive au 9ème barreau de l'échelle. Sachant que les barreaux sont espacés de 30 cm et que le niveau de l'eau monte de 40 cm par heure, quel barreau l'eau aura-t-elle atteint au bout de trois heures ? Cette énigme rappelle beaucoup celle du récipient qui fuit, on peut donc être tenté de procéder de la même façon en faisant le point jour après jour.
| Niveau | Barreau | ||||
| Départ | 9ème barreau (à 0 cm) | ||||
| Heure 1 | 40 cm | 8ème barreau (à 30 cm) | |||
| Heure 2 | 80 cm | 7ème barreau (à 60 cm) | |||
| Heure 3 | 120 cm | 5ème barreau (à 120 cm) |
Comme le 6ème barreau n'est qu'à 90 cm du niveau de départ, l'eau dépasse allègrement ce barreau durant la troisième heure et atteint même tout juste le niveau du 5ème barreau.
Mais en réalité ce raisonnement est totalement faux car il ne peut pas s'appliquer aux conditions du problème. Il y a en effet une astuce toute bête à comprendre. La corde est placée sur le flanc d'un bateau, or un bateau flotte... Donc l'eau aura beau monter autant qu'elle veut, le bateau flottera toujours et le niveau de l'eau ne dépassera jamais celui de départ. La réponse est donc 9.


Enigme 125 : Dé codé (60 picarats)
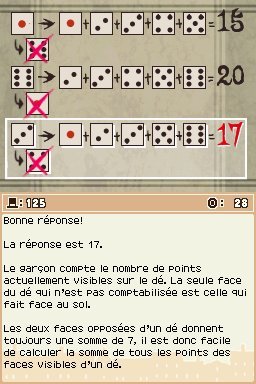
Un garçon s'amuse à lancer un dé et, à chaque fois qu'un chiffre sort, il prononce un nombre différent : 15 pour 1, et 20 pour 6. Il faut essayer de comprendre son raisonnement pour deviner ce qu'il dira lorsque le dé indiquera le chiffre 3. C'est assez tordu mais le garçon compte en fait le nombre de points qu'il peut voir une fois le dé lancé. Cela inclut donc 5 faces puisque la seule qu'il ne peut pas voir est celle qui est tournée contre le sol. Si on sait que la somme de deux faces opposées d'un dé est toujours égale à 7, le calcul devient très simple. Il suffit d'ajouter 14 (la somme des deux groupes de faces opposées qui sont visibles) au chiffre indiqué par le dé.
14 + 1 = 15
14 + 6 = 20
14 + 3 = 17
La solution est donc 17.

Enigme 126 : En rouge et bleu (2) (70 picarats)
On retrouve à nouveau le problème des boules rouges à placer à droite et des boules bleues à placer à gauche, avec seulement un intervalle pour les échanger. Le problème est complexifié par le fait qu'on nous impose de ranger les boules dans l'ordre alphabétique, ABCD, dans chaque zone. La solution vous est donnée en 45 mouvements sur cette vidéo.
Si on numérote les emplacements comme ceci :
| X1 | Y1 | ||||
| X2 | N | Y2 | |||
| X3 | O | S | E | Y3 | |
| X4 | Y4 |
La solution pas à pas est la suivante (le signe '>' signifie "vers") :
1. X3 > E
2. X2 > N
3. X1 > O
4. X4 > X1
5. O > X4
6. N > X2
7. X4 > N
8. E > X4
9. Y3 > X3
10. Y4 > O
11. N > Y4
12. Y2 > N
13. Y1 > S
14. Y4 > Y1
15. S > Y4
16. N > Y2
17. Y4 > N
18. O > Y4
19. X3 > Y3
20. X4 > E
21. N > X4
22. X2 > N
23. X1 > O
24. X4 > X1
25. O > X4
26. E > X2
27. Y3 > X3
28. Y2 > O
29. N > Y2
30. O > N
31. X3 > Y3
32. X2 > E
33. N > X2
34. X4 > N
35. E > X4
36. Y3 > X3
37. Y4 > O
38. N > Y4
39. O > N
40. X3 > Y3
41. X4 > E
42. N > X4
43. E > N
44. Y3 > X3
45. N > Y3
Sommaire de la soluce de Professeur Layton et L'Étrange VillageSommaire de la soluce des défis de Professeur Layton et L'Étrange Village