Page issue de la soluce de Professeur Layton et l'Étrange Village.

Trouvez les 20 petites bricoles pour débloquer ces trois énigmes bonus.

Maison du bricoleur

Enigme 121 : Au coeur du drapeau (60 picarats)

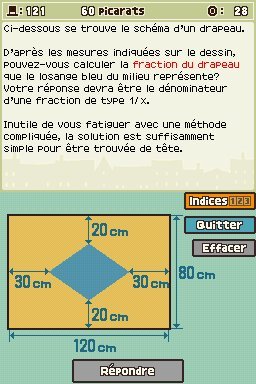
On vous montre le schéma d'un drapeau constitué d'un losange bleu sur fond jaune. A l'aide des dimensions indiquées sur le dessin, vous devez essayer de calculer quelle fraction du drapeau le losange bleu représente. La réponse doit être le dénominateur d'une fraction de type 1/x. On vous indique également que le problème ne requiert pas de calculs compliqués et que la solution peut être trouvée de tête.

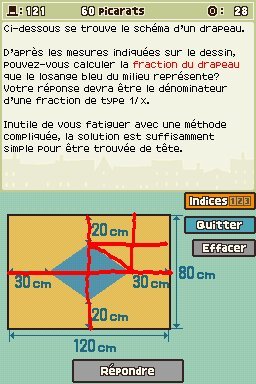
Plutôt que d'utiliser les mesures indiquées en cm, on va donc se contenter de manipuler uniquement les fractions. Si on découpe le drapeau en quatre rectangles, chaque rectangle contient un quart du losange. Autrement dit, la fraction que l'on cherche est la même que la fraction que représente le quart du losange sur le quart du drapeau.

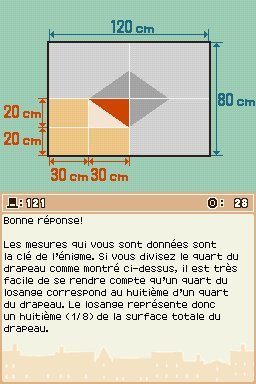
Prenons donc juste l'un des quatre rectangles qui représente un quart du drapeau et coupons-le à nouveau en quatre. Cette fois, la partie du losange qui nous intéresse est égale à la moitié d'un quart du rectangle, soit 1/2. Il n'y a donc plus qu'à diviser par 4 (ou multiplier par 1/4) pour obtenir le résultat sur l'ensemble du rectangle : 1/2 x 1/4 = 1/8.

Et, comme on l'a dit plus haut, cette fraction est la même que celle du losange entier sur le drapeau entier (un quart du losange correspond au huitième d'un quart du drapeau). Le résultat est donc 8, puisque c'est uniquement le dénominateur de la fraction qu'on nous demande.

Enigme 122 : Suite de dés (60 picarats)

Des dés sont alignés de manière à constituer une suite logique. Vous devez trouver quel est le dé à placer ensuite. Il faut donc d'abord comprendre la logique qui régit cette suite de 3 et de 6, disposés d'une certaine façon. Leur orientation a une importance.

Pour ce qui est du 3, par exemple, on voit bien que les points sont alignés de manière à former une ligne continue, de dé en dé. Mais cette logique se brise au niveau des 6. Il faut donc chercher ailleurs.

La clé se trouve dans le fait que les dés forment un ensemble de points qui sont répartis sur trois lignes. Si on observe en particulier la ligne du haut et qu'on compte le nombre de points adjacents, on constate qu'ils forment une suite logique : 1, 2, 3, 4, puis 5 points adjacents, chaque groupement étant séparé par un ou plusieurs blancs.

Le prochain chiffre attendu est donc un 6, et comme on en a déjà trois, il suffit d'en rajouter trois autres, ce qui oblige à choisir le dé C qui est le seul à présenter trois points sur la rangée du haut. La réponse est donc C.

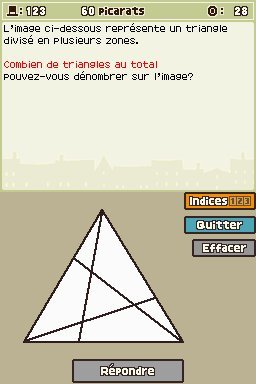
Enigme 123 : Tant de triangles ! (60 picarats)

Une image représente un triangle divisé en plusieurs sections. On vous demande de dénombrer combien il y a de triangles différents sur cette image. Il y a déjà le premier triangle englobant les autres (1).

Il y en a 4 petits dans les sections intérieures au triangle (1 + 4 = 5). Il faut aussi rajouter les triangles intermédiaires formés par deux ou trois petites sections.

On en voit 2 qui partagent les sommets situés en haut et à gauche, 3 qui partagent les sommets situés en haut et à droite, et 3 autres qui partagent les sommets situés à gauche et à droite, ce qui nous en fait rajouter 8, soit déjà : 5 + 8 = 13 triangles.

Mais il en manque encore. Il s'agit des triangles qui ne partagent qu'un seul sommet avec le triangle global. Si on enlève ceux qui ne sont constitués que d'une seule section, on peut en voir 1 qui longe le bord gauche, 2 qui longent le bord inférieur, et 1 qui longe le bord droit du grand triangle, soit 4 de plus (13 + 4 = 17). Il y a donc 17 triangles en tout sur cette image.