Page issue de la soluce de Professeur Layton et l'Étrange Village.
Chapitre 6 - La tour mystérieuse
Objectif : Trouvez la route de la tour.
Montez vers la grand-place.
Grand-place
Parlez à Percy.
Enigme 072 : Propos fallacieux (40 picarats)
A nouveau, vous devez trouver qui ne ment pas parmi un groupe de personnes. On peut une fois encore procéder par élimination. Si A dit vrai et que les autres mentent, ça voudrait dire que B dit aussi la vérité (selon C), ce qui est impossible. Si c'est B qui dit vrai, les mensonges des deux autres tiennent la route. Enfin, si C dit vrai, alors A dirait aussi la vérité (selon B), ce qui est impossible. Il n'y a donc que B qui ne ment pas.


Vous obtenez une lampe de bureau (H18/30) à donner à Luke. Franchissez la porte bleue.
Mairie
Parlez à Rodney.
Enigme 073 : Histoire de carrés (40 picarats)
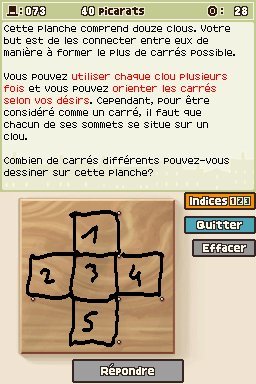
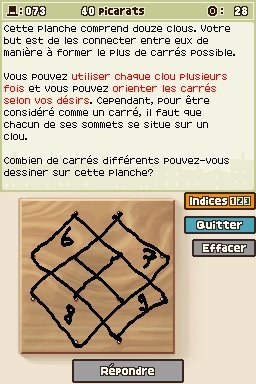
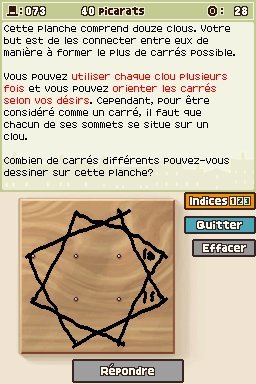
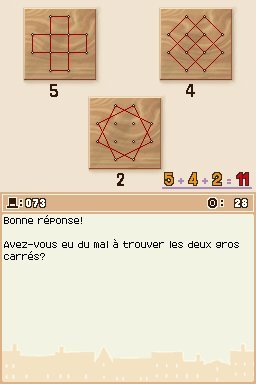
Combien de carrés différents peut-on dessiner sur une planche comportant douze clous ? Il y a déjà les 5 petits formant une croix. Ce sont les seuls qu'on puisse obtenir en laissant la planche dans ce sens. Si on tourne la planche à 45°, on peut en trouver d'autres en traçant des diagonales entre les clous. Il y en a 4 qui, ensemble, forment également une croix. Mais il en reste encore deux, un peu plus difficiles à voir. Ils s'obtiennent en reliant deux fois 4 points situés sur les bords de la planche. Lorsque vous tracez ces deux carrés, ils forment une étoile à huit branches. Au total, on obtient donc 11 carrés différents (5 + 4 + 2).
Vous obtenez un gramophone (H19/30) à donner à Layton. Quittez cette pièce, allez vers la tour de l'horloge, puis prenez à gauche au croisement.
Marché
Parlez à Agnès.
Enigme 074 : Une vitre cassée (30 picarats)
Quatre enfants étaient en train de jouer lorsque l'un d'eux a cassé une vitre en lançant sa balle. L'un des quatre ment mais ce n'est pas le seul menteur, et vous devez néanmoins trouver qui a réellement cassé la vitre. La difficulté vient du fait qu'on ne sait pas combien il y a de menteurs sur les quatre. On ne va donc pas procéder comme précédemment en passant en revue ceux qui disent la vérité, mais on va plutôt voir s'il y a une contradiction avec le fait que celui qui a cassé la vitre ment.
Si A a cassé la vitre, il ment bien, et peu importe ce que disent les autres. Si B a cassé la vitre, son mensonge serait : "j'ai cassé la vitre", ce qui n'est pas possible. Si c'est C qui a cassé la vitre, il prétend alors que c'est A qui l'a cassée, ce qui est impossible. Enfin, si c'est D, ses propos dénoncent B comme étant le coupable, ce qui est impossible. A partir du moment où il n'y a qu'un coupable et où le coupable ment, ça ne peut être que A.


Parlez de nouveau à Agnès.
Enigme 075 : Avec du fil de fer (40 picarats)
Vous disposez de fils de fer avec lesquels vous devez construire un cube. De combien de fils au minimum aurez-vous besoin, sachant que vous ne pouvez pas faire passer plus d'un fil sur une arête du cube ? En vous aidant du dessin, essayez de tracer le chemin le plus long sans vous arrêter.
A partir du coin inférieur gauche, par exemple, vous pouvez faire les trois arêtes de cette première face, puis les deux arêtes suivantes de la face de droite, puis les deux suivantes de la face arrière droite, puis encore deux sur la face posée sur la table.
Malheureusement, bien qu'il ne reste plus que 3 arêtes, elles ne sont pas adjacentes et vous aurez donc besoin de 3 fils supplémentaires pour les terminer. Quelle que soit la manière dont vous essaierez, vous vous retrouverez toujours avec au moins 4 fils à utiliser. C'est donc la bonne réponse.


Vous obtenez un globe (H20/30) à donner à Luke. Avancez vers le nord.
Passage sombre
Pièce 1 : La lucarne de la grande porte.
Pièce 2 : Les fleurs du vase de droite.
Pièce 3 : Sur le rebord à droite.
Pièce 4 : Au sol, près de la marche.
Cliquez sur l'enseigne rouge, en hauteur.
Enigme 119 : En rouge et bleu (1) (40 picarats)
Des boules rouges et bleues sont disposées dans leurs emplacements opposés. Vous devez les remettre comme il faut en les déplaçant à l'aide du stylet. Vous ne bénéficiez que d'un seul espace pour les faire changer de côté. En tâtonnant, le résultat n'est pas compliqué à obtenir. Il faut juste penser à glisser les boules correctement placées en les rangeant du haut vers le bas, et à faire transiter parfois trois boules en même temps sur la ligne horizontale. Voici une méthode en vidéo pour réussir cette épreuve en seulement 30 coups.
Si on numérote les emplacements comme ceci :
| X1 | Y1 | ||||
| X2 | N | Y2 | |||
| X3 | O | S | E | Y3 | |
| X4 | Y4 |
La solution pas à pas est la suivante (le signe '>' signifie "vers") :
1. Y3 > N
2. X3 > Y3
3. X4 > E
4. N > X4
5. E > X3
6. Y3 > O
7. Y4 > N
8. O > Y4
9. X3 > Y3
10. X2 > E
11. X1 > O
12. X4 > X1
13. O > X4
14. N > X2
15. E > X3
16. Y3 > O
17. Y2 > N
18. Y1 > E
19. Y4 > Y1
20. E > Y4
21. O > Y2
22. X3 > Y3
23. X4 > E
24. N > X4
25. E > X3
26. Y3 > O
27. Y4 > N
28. O > Y4
29. X3 > Y3
30. X3 > Y3
Continuez vers le nord.
Route de la tour
Pièce 1 : La fenêtre de la maison du fond.
Pièce 2 : La mousse sous la fenêtre de gauche.
Pièce 3 : Les fleurs de droite.
Pièce 4 : La lanterne au-dessus de la porte.
Ramassez le papier posé par terre et parlez à Martha.
Enigme 102 : As et joker (40 picarats)
Un paquet de 52 cartes ainsi qu'un joker sont posés sur une table face cachée. Si vous retournez les cartes une par une, quel est le pourcentage de chance que vous trouviez les 4 as avant le joker ? Autrement dit, quel est le pourcentage de chance de trouver le joker après les 4 as ? A première vue, on peut penser que le résultat sera du style x/53, puisqu'il y a 53 cartes au total. Mais comme les cartes autres que le joker et les as n'entrent pas en compte dans le problème, on peut faire comme si on avait seulement 5 cartes en tout. A partir de là, on n'a plus qu'une chance sur cinq de tirer le joker plutôt qu'un as. La solution est donc 20% ((1x100)/5 selon la règle de 3).


Cliquez sur la fenêtre ouverte à droite.
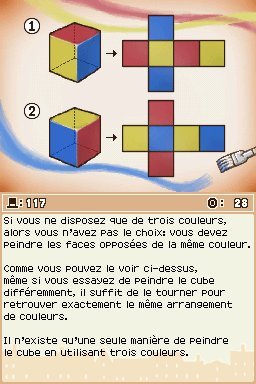
Enigme 117 : Cube à peindre (30 picarats)
On vous demande de peindre un cube en papier avec trois couleurs en faisant en sorte que deux faces de même couleur ne soient jamais en contact l'une avec l'autre. Combien d'arrangements différents pouvez-vous obtenir en respectant ces conditions ? Le plus simple est de dessiner le patron du cube. Si vous placez une couleur à un endroit, vous ne pourrez utiliser à nouveau cette même couleur que sur la face opposée. Essayez de numéroter chaque face du patron en respectant cette condition et vous obtiendrez un seul résultat possible. Tout ce que vous pouvez faire ensuite c'est remplacer les numéros par n'importe quelle couleur, mais ça reviendrait à reproduire toujours le même schéma avec des couleurs différentes, ce qui est interdit. Il n'y a donc qu'un seul arrangement possible.

Continuez vers le nord. La jeune fille fait tomber un ticket que vous récupérez et vous terminez le chapitre.
Fin du chapitre 6
Objectif : Rendez-vous au parc.
Cul-de-sac
Pièce 1 : La petite fenêtre en hauteur.
Pièce 2 : La mousse en bas à gauche.
Pièce 3 : Le point juste au-dessus de la chaussure en bas à droite.
Pièce 4 : Le bas du toit en haut à gauche.
Revenez sur vos pas jusqu'au marché, puis allez à droite.
Belvédère
Pièce 1 : La lucarne du toit gris.
Pièce 2 : Le petit arbre à côté du toit de gauche.
Continuez vers le sud jusqu'à la grand-place, puis allez à gauche.
Route du parc
Pièce 1 : Le muret du fond, à droite de la grille.
Parlez à Paulo.
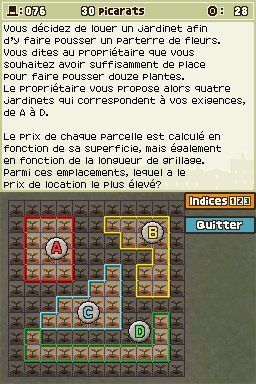
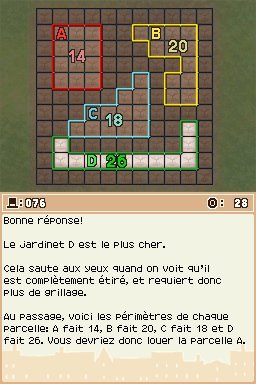
Enigme 076 : Les quatre jardins (30 picarats)
Quatre parcelles de terrain permettant chacune de faire pousser 12 plants vous sont proposées. Sachant que le prix d'une parcelle est calculé en fonction de sa superficie et de la longueur de grillage, quelle est celle qui a le prix de location le plus élevé ? Les quatre parcelles diffèrent seulement par leur forme, pas par leur superficie, vous devez donc uniquement tenir compte de la longueur du grillage, et donc du périmètre de chaque aire. Il suffit donc de compter le nombre de petits traits colorés qui entourent chaque parcelle. A = 14, B = 20, C = 18 et D = 26. C'est donc la D la plus chère.
Parlez à Adrea.
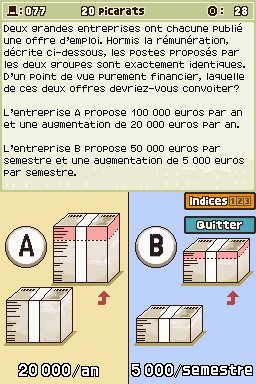
Enigme 077 : Offres d'emploi (20 picarats)
Pour un même travail, deux offres d'emploi proposent des rémunérations différentes. L'entreprise A vous paye 100 000 euros par an avec une augmentation de 20 000 euros par an. L'entreprise B vous paye 50 000 euros par semestre avec une augmentation de 5 000 euros par semestre. Quelle est la plus avantageuse ? Il va falloir comparer les salaires obtenus sur une année, puis sur une deuxième année pour visualiser l'évolution.
Année 1 :
A = 100 000
B = 50 000 + 55 000 = 105 000
Année 2 :
A = 100 000 + 20 000 = 120 000
B = 60 000 + 65 000 = 125 000
Attention à ne pas vous tromper pour l'année 2. En B, l'année 2 commence avec un troisième semestre, il faut donc partir de 60 000 et pas de 55 000. L'offre la plus avantageuse à long terme est donc la B.

Vous obtenez une plante verte (H21/30) à donner à Layton. Franchissez la porte bleue.
Restaurant
Pièce 1 : Le lustre de droite.
Parlez à Michel.
Enigme 078 : Problème aqueux (60 picarats)
Transvasez 16 litres d'eau à l'aide de 3 récipients de 16 litres, 9 litres et 7 litres pour obtenir deux fois 8 litres. Procédez comme suit : 16>9, 9>7, 7>16, 9>7, 16>9, 9>7, 7>16, 9>7, 16>9, 9>7, 7>16, 9>7, 16>9, 9>7, 7>16 pour réussir en 15 coups seulement.
Vous obtenez un bouquet de fleurs (H22/30) à donner à Layton. Parlez de nouveau à Michel.
Enigme 079 : Transfert de fruits (40 picarats)
Six caisses jaunes et six caisses rouges ont été inversées. Vous devez les remettre dans leurs emplacements respectifs en les faisant glisser à l'aide du stylet et en utilisant les deux cases libres pour les faire transiter. Vous avez déjà vu ce problème auparavant, mais il y avait deux fois moins d'éléments à déplacer. Comme précédemment, on y arrive sans difficulté en tâtonnant, mais cette vidéo montre comment le réussir en seulement 26 coups.
Si on numérote les emplacements comme ceci :
| X1 | X4 | N | Y1 | Y4 | |||
| X2 | X5 | O | C | E | Y2 | Y5 | |
| X3 | X6 | S | Y3 | Y6 |
La solution pas à pas est la suivante (le signe '>' signifie "vers") :
1. X5 > S
2. X4 > N
3. Y2 > X4
4. Y1 > X5
5. Y4 > O
6. N > Y4
7. S > Y1
8. O > Y2
9. X5 > E
10. X2 > S
11. X1 > N
12. E > X1
13.
{{uppage}}Y2 > X2
14. Y5 > X5
15. Y6 > O
16. N > Y6
17. S > Y5
18. O > Y2
19. X5 > E
20. X6 > N
21. X3 > S
22. E > X3
23. Y2 > X6
24. Y3 > X5
25. N > Y3
26. S > Y2
Vous obtenez un morceau de tableau (T14/20). Parlez à Boris.
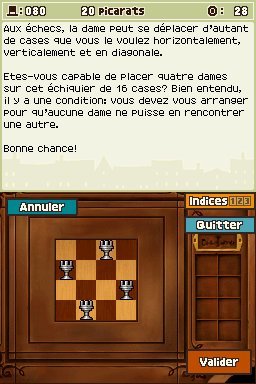
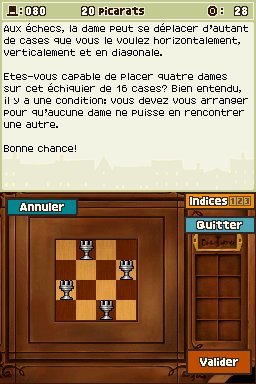
Enigme 080 : Dames en folie (1) (20 picarats)
Quatre dames doivent être placées sur un petit échiquier de manière à ce qu'aucune dame ne puisse en rencontrer une autre. Vous devez évidemment respecter les mouvements de la dame lors d'une partie d'échecs, celle-ci pouvant se déplacer aussi bien en diagonale que verticalement ou horizontalement. L'exercice n'est pas aussi simple qu'il en a l'air. En toute logique, il devrait y avoir une dame par ligne et par colonne, ça devrait suffire à vous aiguiller. Vérifiez que vous n'avez aucune pièce sur un coin de l'échiquier ni sur l'une des quatre cases centrales, et que la figure obtenue est symétrique. Vous obtiendrez alors le résultat visible sur cette image et sur ce schéma.
| - | - | x | - | |
| x | - | - | - | |
| - | - | - | x | |
| - | x | - | - |
ou :
| - | x | - | - | |
| - | - | - | x | |
| x | - | - | - | |
| - | - | x | - |
Vous obtenez un fauteuil (H23/30) à donner à Layton. Parlez de nouveau à Boris.
Enigme 081 : Dames en folie (2) (40 picarats)
Le même problème, mais avec un échiquier de 25 cases et 5 dames à placer. Cette fois vous ne pouvez pas appliquer les astuces de l'énigme précédente. Il existe plusieurs solutions possibles, cette image et ce schéma vous en donnent une. Si vous placez la première dame au centre de l'échiquier, le résultat est assez facile à obtenir.

| - | x | - | - | - | |
| - | - | - | - | x | |
| - | - | x | - | - | |
| x | - | - | - | - | |
| - | - | - | x | - |
Vous obtenez un morceau de tableau (T15/20). Parlez une fois de plus à Boris.
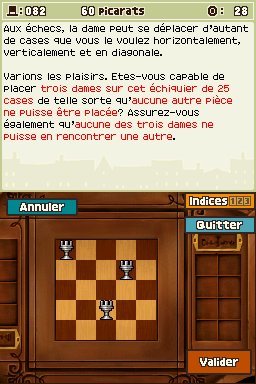
Enigme 082 : Dames en folie (3) (60 picarats)
C'est reparti pour un tour. L'échiquier n'a pas changé mais les données du problème sont différentes. Non seulement vous devez faire en sorte qu'aucune des trois dames ne puisse se rencontrer, mais vous devez aussi vous arranger pour qu'on ne puisse placer aucune autre pièce. Autrement dit, chacune des cases de l'échiquier doit être sur la trajectoire d'une des trois dames. Voici la solution.
| x | - | - | - | - | |
| - | - | - | x | - | |
| - | - | - | - | - | |
| - | - | x | - | - | |
| - | - | - | - | - |
Vous obtenez un porte-chapeaux (H24/30) à donner à Layton. Parlez une dernière fois à Boris.
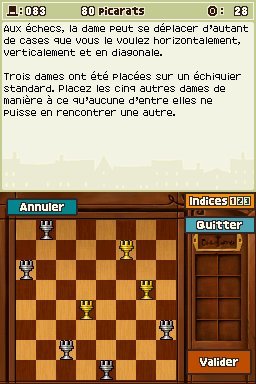
Enigme 083 : Dames en folie (4) (80 picarats)
Retour aux conditions de base : il faut placer toutes les dames de sorte qu'elles ne puissent pas se rencontrer. L'échiquier possède maintenant 64 cases, 3 dames sont déjà en place et vous devez en rajouter 5. Voici la seule et unique solution.
| - | x | - | - | - | - | - | - | |
| - | - | - | - | -D | - | - | ||
| x | - | - | - | - | - | - | - | |
| - | - | - | - | - | - | D | - | |
| - | - | - | D | - | - | - | - | |
| - | - | - | - | - | - | - | x | |
| - | - | x | - | - | - | - | - | |
| - | - | - | - | x | - | - | - |
Vous obtenez un morceau de tableau (T16/20). Quittez le restaurant et allez au nord.
Grille du parc
Pièce 1 : Au centre du muret de gauche.
Poussez la grille pour passer au chapitre suivant.
Sommaire de la soluce de Professeur Layton et L'Étrange VillageSommaire de la soluce de l'aventure principale de Professeur Layton et L'Étrange Village