censée*

Je t'envois le screen de l'exo

https://pbs.twimg.com/media/Ba9pUPWCcAEdsa0.jpg

Toujours le bug

Ton lien marche pas..

| https://www.jeuxvideo.com/forums/1-50-147943120-121-0-1-0-je-fais-vos-devoirs-en-maths-v2.htm#message_151346968
| Ecrit par « The_Kil_Bis », 4 décembre 2013 à 15:19:09
| « Bonjours Dowie, j'ai un dm a faire en voici un exo :
|
|
| Dans cette exercice, f et g désignent respectivement la fonction carré et la fonction inverse, Cf et Cg leurs courbe représentative dans un repère ( O; I; J ) ( I et J sont des vecteurs )
|
| On se propose de mettre en evidence deux pp géométriques des tangentes à Cf et Cg.
|
| 1. Tangante à une parabole
|
| Soit a et b deux réels distincts et soit A et B de Cf d'abscisses a et b.
|
| a. Déterminer les équations des tangentes Ta et Tb à Cf aux pts d'abscisses a et b.
| b. Montrer que les droites Ta et Tb sont sécantes et déterminer les cord. de leur pts d'intersection K
| c. Soit L milieu de [AB]. Déterminer les cord. de L puis démontrer que la droite (KL) est parallèle à l'axe des ordonnées.
| d. Démonter que le milieur M du segment [KL] appartient a Cf et que la tangente à Cf en M est parallèle à la droite (AB)
| e. En déduire un procédé simple permetta,t de construire la tangante à Cf en un pts donné.
|
| Voilà, de ton aide »

dowie

Bonjour,

Soit f(x)=Somme de n=E(|x|) à +infini de arctan(x²/n²), où désigne la partie entière.

1/Quel est le domaine de définition de f ?
2/Étudier la continuité de f. Que vaut [lim(f(t))(t->x par valeur supérieure) - lim(f(t))(t->x par valeur inférieure)], si x est un point de discontinuité de f ?
3/Déterminer lim(f(x))(x->+infini)

Merci

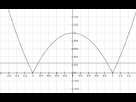
Je dois determiner l'equation du graph
Mais comment ?

the-awesome-miz f(x)= |x^2|

Oh my bad c'est : |x^2 - 1|

Désolé !

Merci beaucoup

hybrid ==> arctan(x²/n²) ~ x²/n² donc la série converge pour tout x

f continue sur les ]n;n+1[ suffit d'appliquer le théorème de continuité sur les séries sur un tel intervalle (série qui converge normalement)
f est non continue en n € N!

cette limite est sauf erreur -arctan(n²/(n-1)²) =/= 0 (attention il faut utiliser le théorème d'inversion limite somme mais par convergence normale ça marche bien)

Merci beaucoup !

Hum test ?

merci

Bonjours Dowie, j'ai un dm a faire en voici un exo :

Dans cette exercice, f et g désignent respectivement la fonction carré et la fonction inverse, Cf et Cg leurs courbe représentative dans un repère ( O; I; J ) ( I et J sont des vecteurs )

On se propose de mettre en evidence deux pp géométriques des tangentes à Cf et Cg.

1. Tangante à une parabole

Soit a et b deux réels distincts et soit A et B de Cf d'abscisses a et b.

a. Déterminer les équations des tangentes Ta et Tb à Cf aux pts d'abscisses a et b.
Soit x appartenant à R
f'(x) = 2x
La tangente à Cf en a, a donc pour équation:
y = f'(a)(x-a) + f(a) = 2a(x-a) + a^2 = 2ax - a^2
De même la tangente en b a pour équation
y = 2bx - b^2

b. Montrer que les droites Ta et Tb sont sécantes et déterminer les cord. de leur pts d'intersection K
Soit K(x,y)
y = 2ax - a^2
y = 2bx - b^2
<=>
0 = 2(a-b)x - a^2+b^2
y = 2bx - b^2
<=>
x = (a^2-b^2)/(2(a-b)) car a-b =/=0
y =2bx - b^2
<=>
x = (a-b)(a+b)/(2(a-b)) = (a+b)/2
y = 2b*(a+b)/2 - b^2 = ab

Les coordonnées de la sécante sont ((a+b)/2 , ab )

c. Soit L milieu de [AB]. Déterminer les cord. de L puis démontrer que la droite (KL) est parallèle à l'axe des ordonnées.
A a pour coordonnées (a,a^2)
B a pour coordonnées (b,b^2)
donc L a pour coordonnées ( (a+b)/2 , (a^2 + b^2)/2)
->KL a pour coordonnées ( (a+b)/2 - (a+b)/2 , (a^2+b^2)/2 - ab )
= (0, ((a-b)^2) /2 ) avec a=/=b : (KL) est parallèle à l'axe des ordonnées

d. Démonter que le milieur M du segment [KL] appartient a Cf et que la tangente à Cf en M est parallèle à la droite (AB)
M a pour coordonnées ( (a+b)/2 , 1/4 ( a^2 +b^2) + ab/2 ) )
ce qui vaut ( (a+b)/2 , 1/4 * (a+b)^2 )
cad ((a+b)/2 , f((a+b)/2 )
donc M appartient à Cf

f'( (a+b)/2 ) = a+b
Or ->AB a pour coordonnées (b-a , b^2-a^2)
Ce qui donne comme coefficient directeur pour (AB) : (b^2 -a^2)/(b-a) = a+b

Le coefficient directeur de (AB) est f'((a+b)/2) donc la tangente en M est parallèle à (AB)

e. En déduire un procédé simple permetta,t de construire la tangante à Cf en un pts donné.

Le procédé simple c'est :
si on veut trouver la tangente en un point t : on prend deux valeurs a et b assez éloignée telles que t =(a+b)/2
. On pose A (a, f(a) ) , B(b, f(b) ).

On a juste à tracer la parallèle à (AB) passant par le point (t, f(t)) pour avoir la tangente au point d'abscisse t

Super

J'avais trouvé les equations et je n'arrivais pas a montrer qu'elle se coupait

Je dois trouver le PGCD de 45 et 86 perso.. (3ème)

86 = 45 + 41
45 = 41 + 4
41 = 4*10 + 1
4 = 4*1
Le PGCD est 1